现存问题 (WHY:为什么需要改进)

目前主流的联盟链平台采用的都是全复制的存储策略，即：每个节点都要维护所有的历史数据。

因此，当链上的数据量和系统中的节点数量增多时，每个节点都必须支付昂贵的存储花销，系统可扩展性也会大幅下降，随着需求和用户数量的不断膨胀，区块链平台将难以再满足服务需求。

可能改进方案
- 降低链上数据的存储花销——减少存储量
- 数据块进行编码后再由每个节点存储一部分的编码值，同时提升系统编码、解码时的计算效率——降低通信量

传统方案

硬盘空间回收
- 如果一笔交易存储在足够多的区块，该交易之前的数据可以删除
- 因为默克尔根没有更改，所以仍然可以验证默克尔根完成交易验证
- 👎如果要恢复原始的数据，可能无法恢复。只能做验证
链下存储
- 区块体存在链下，通过唯一标识可访问
- 常见方案：分布式哈希表（DHT）、基于星际文件系统（IPFS）的链下存储、基于云的链下存储
  - 分布式哈希表（DHT）:形成键值对，键为通过哈希函数生成的唯一性数据标识，值为区块体
  - 基于星际文件系统（IPFS）：存储在去中心化的IPFS网络中, 数据被分割成小块，并为每个数据块生成唯一的哈希值，可以根据哈希和链表拿到全部的数据
  - 将数据存储在云服务提供商的存储系统中
链上存储模式
- 常见方案：协作式存储和轻节点存储
  - 继续细分：基于编码的协作式存储、基于分片的协作式存储和基于集群的协作式存储
    - 协作式存储：每个节点负责存储一部分数据（类似于IPFS）
      
      轻结点存储：它允许轻节点只存储特定的数据块或元数据，而非全量数据。（如以患者为中心的细粒度访问控制，通过双区块链安全共享电子病历的病人，无需存储每一次交易、双区块链辅助条件下隐私保护认证与车载网协议的车辆无需存储每一次车辆事故）

技术介绍

纠删码技术

简单总结：将数据分为n片，只需要f片就可以恢复元数据

有点类似于门限签名，见[[../../学习/区块链/Hotstuff相关的改进]]

RS编码

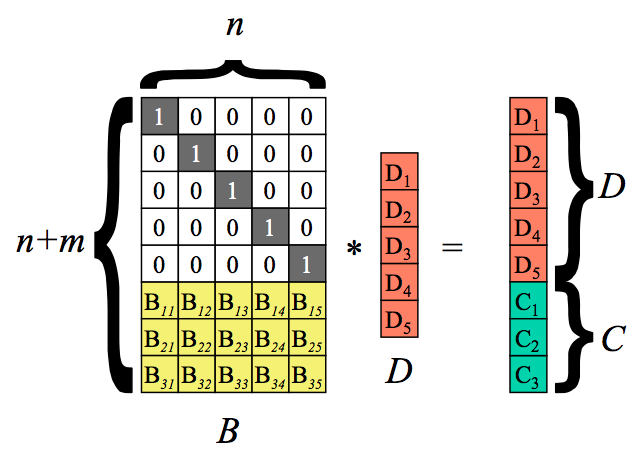
范德蒙 RS 编码

这篇文章介绍的是列向量为数据块，论文使用的行向量，实质是一样的

$D$即是数据块、$C$即是校验块，等号右边为编码后的编码块

处理步骤：

选择$n$个编码字（$\alpha_0,\alpha_1,…,\alpha_{n-1}$），作为编码矩阵（即上图矩阵$B$）。
$k$个数据字（$m=\{m_0、m_1、…、m_{k-1}\}$）编码可以得到$(k,n)-RS$
$(k,n)-RS$满足—— $f_m(X)=\sum_{i=0}^{k-1}m_iX^i \quad (X=\alpha_0,\alpha_1,...,\alpha_{n-1})$
编码字组合可以得到编码块 $RS(m)=(f_m(\alpha_0),f_m(\alpha_1),...,f_m(\alpha_{n-1}),)$
每个结点$Node_i$存储对应的编码字$f_m(\alpha_i)$
服务器仅需收集$n$中任意$k$个编码字即可恢复，即使解如下方程
- 目的：求解$k$个数据字（$m=\{m_0、m_1、…、m_{k-1}\}$）
- 已知：$k$个方程，$k$个未知量，因此可以求解

如果写成矩阵形式，那么编码矩阵$X_i$可以表示为
$\begin{pmatrix} 1 &1& \cdots & 1 \\ \alpha_0 & \alpha_1& \cdots & \alpha_{n-1} \\ \alpha_0^2 & \alpha_1^2& \cdots & \alpha_{n-1}^{2}\\ \vdots & \vdots & \ddots &\vdots \\ \alpha_0^{k-1} & \alpha_1^{k-1}& \cdots & \alpha_{n-1}^{k-1} \end{pmatrix}$
那么RS就可以表示为
$RS=(m_0,m_1,\cdots,m_{k-1})\begin{pmatrix} 1 &1& \cdots & 1 \\ \alpha_0 & \alpha_1& \cdots & \alpha_{n-1} \\ \alpha_0^2 & \alpha_1^2& \cdots & \alpha_{n-1}^{2}\\ \vdots & \vdots & \ddots &\vdots \\ \alpha_0^{k-1} & \alpha_1^{k-1}& \cdots & \alpha_{n-1}^{k-1} \end{pmatrix}$
即一个$k$维行向量（数据块）与编码矩阵相乘，即可得到$n$维行向量，即编码块

性能瓶颈：矩阵求逆和矩阵乘法上有限制

柯西编码

在范德蒙的基础上，以可惜矩阵作为编码矩阵

$cauchy=\begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{(k-1)1} & a_{(k-1)2} & \cdots & a_{(l-1)n} \\ a_{k1} & a_{k2} & \cdots & a_{kn} \\ \end{pmatrix}$

其中$a_{ij}=\frac{1}{x_1-y_j}(x_1\neq y_j)$，最后每个元素都是0或者1
通过位运算转换方法将域上的乘法运算转化为二进制抑或XOR运算

其中的$a$不同于范德蒙的$\alpha$，后者是直接从$GF(2^w)$的元素选，前者（本部分）是元素经过变换得到
这样把实际的数字转换为0/1二进制，用抑或代替乘法，实现了高效的求解

RS编码的联盟链设计（WHAT）

核心思想

区块->分片&编码->签名&全网共识
结点仅存储部分共识后的编码值

数据分片

传统的BFT-Store方案——
每$N-2F$个区块打包成组，再通过RS编码形成N个区块【即$(N-2F,N)-RS$】
但是读取一个区块需要恢复这组全部区块
改进：对每个区块进行分片

编码和解码复杂度受到$l$编码字长度的影响（求解的时候位移和抑或的位数更多）
改进：采用多级分片，控制数据分片再1kb以内

符号说明：

$B(h)$:区块的哈希

$f_{h,i}(s)$:第i个以及分片的第$s$个编码值

二级分片编码后得每个$N_i$给第$i$个结点存储

分片数量的确定

$\frac{区块大小}{一级分片数量·二级分片数量}=二级分片大小l<1kb$

二级分片的数量$k$不小于$N-2F$
- $k=N-F(正常节点存储)>F(恶意结点存储)$
- 为了避免冗余即取最小值
一级分片数量可以计算得$2^8$
- 假设区块大小1MB，节点数100，恶意节点33

数字签名

需要对分片进行数字签名，代表认可分片
无证书的聚合签名方案 CLAS 方案认证编码值

签名时间

PBFT几个阶段
在commit阶段起点(结点已经达成共识)对新区块所有编码值签名（包括无需存储得）

然后随着commit继续广播

验证&聚合签名

签名是对每一个编码矩阵$f_{h,i}(s)$签名，而不是对每一个二级分片的每一项签名

受到其他结点得commit消息后，验证签名合法性->签名正确即信任代表编码正确

第一次聚合签名：收到$F+1$个合法commit（超过三分之一），聚合所有签名$\sigma_{h,i,s}$.

第二次聚合：对于收到的$σ_{h,1,s}, σ_{h,2,s}, …, σ_{h,r,s}$进行聚合为$\sigma_{h,s}$，$\sigma_{h,s}$存储在自己保存的编码值

最终保存的内容有：

聚合签名：代表所有结点认可了整个分片过程
编码值：比如结点编号1，那么就存储每个二级分片的1号编码值

Require: 节点 Ns、新区块 B(h) 
B = {B1(h), ..., Br(h)} ← Partition(B(h), r) // 分割为r片一级分片
for i from 1 to r do 
	Bi = {bi,1(h), ..., bi,k(h)} ← Partition(Bi(h), k) //对每一一级分片分割二级分片k个
	for j from 1 to N do 
		fh,i(j) ←RSEncode(Bi, N , N − 2F , j) //每一个二级分片RS编码
		Hi ← Hi∪ Sign(fh,i(j), s) //每一个二级分片加上自己的签名
	end for 
	F' ← F' ∪ {fh,i(s)} 
	H' ← H' ∪ Hi //将编码和签名合并到两个变量（这里的合并不是聚合）
	//Hi相当于每个一级分片的签名，H是对整个的签名集合
end for 

将 H' 与 commit 消息一起全网广播 


if 收到 F + 1 个合法的 commit 消息 then 
	H1, ..., HF +1 ← F + 1 个签名集合 //签名分别存储到对应变量
	//如H1存储的1号结点对于所有二级分片签名的集合
	for i from 1 to r do //对每一个二级分片组（一组二级分片对应一个一级分片）
		signs ← {H1[fh,i(s)], ..., HF +1[fh,i(s)]} //找到其他结点对第i个二级分片组的签名集合
		σh,i,s ← Aggregate(signs) //各个其他结点的签名聚合为一个签名，这就是对第i个二级分片组的总签名（第一次聚合）
	end for 
	σh,s ← Aggregate(σh,1,s, ..., σh,r,s) //对每个二级分片组再次聚合（第二次聚合）
	存储该节点对应签名 σh,s 与编码值集合 F ，丢弃其余编码值 
end if

Q：通过hotstuff可不可以进行改进？
A: 可以通过使用hotstuff的门限签名来代替，每个结点对每个二级分片组进行签名，统一发送给hotstuff的leader，如果达成共识，门限签名即可聚合为一个公钥，完成验证。
相比这种方案签名上节省效率更多。

数据恢复

主节点广播“我要获取B(h)的数据”
从结点返回自己存储的编码值（${f_m(\alpha_i)}_a、{f_m(\alpha_i)}_b、\cdots$）和签名
每一个二级分片组可以有如下的方程组——
此时，相当于知道$f_m(\alpha)$,求$m$

因为此时的RS符合 $(N-2F,N)-RS$，所以需要$N-2F$个消息
随后可以得到一级分片的每个数据块$m_a=\{m_0、m_1、m_2、\cdots\}、m_b、\cdots$
一级数据块组合可以得到原始数据

系统重初始化

新节点加入

可以解密
新节点更新其需要保存的编码值

新结点广播“我来了”
旧结点发送自己存储的编码值集合和签名
新结点恢复区块（同[[#数据恢复]]）
应用$(N-2F,N+1)-RS$重新计算所有结点的编码值
对这个编码值全网广播，进行验证和签名（后续同[[#验证&聚合签名]]）
重新编码过程中前 N 个节点所对应保存的编码值集合不变，仅新的结点需要存储新内容。

基本等同于加入的这个新结点对原来的所有区块重新计算编码
——感觉效率有一点点低

这一步可以省略吗？不能，比如初始化n个结点，来了k个，退了k个，如果没有这一步，如果请求退了的k个存有的数据，则无法请求

可否更改策略，使得他们使用同一个RS策略，而不改变RS策略，新来的结点即存储同一个哈希即可。

我的想法💡

设定指定个结点
如果初始结点没有达到这么多，那么轮流着按需存储多余的

比如设置有10RS，初始化只有6个结点，那么多余了4个即只需要存储到1-4号结点
但是这就带来一个问题，相当于1-4号结点在共识有两份投票权
如果新来了一个，就把1号结点的信息发给新的结点
如果超过了，比如计划10RS，那么11号RS就存储和1一样的内容。

这也带来一个问题，相当于对1的共识投票权少一半

既然无法解决投票权的问题，那么我们不如直接预留，刚开始生成RS的时候，即预留足够的分片。如果超出那么再重新初始化。
预留的部分由一个可信结点（如信誉分最高的/主节点） 保存。
视图切换之时进行一次信息传递。

如果主节点是恶意结点，那么重新发起视图切换，重新编码即可。

结点退出系统

退出后仍可解密

无需处理

退出后无法解密

仅在场景2-2（现有结点退出且无法满足解密要求，退出后刚好差一个解密）无法满足

编码方案更新为：
$(N − 2F, N’ − 1)-RS$更新为$((N − 1) − 2F’, N − 1)-RS$

$N’$为当前结点数，包括要退出的结点
拜占庭结点上限$F’=\frac{(N’-1)-1}{3}$ (第二个-1是减去主节点)

对所有区块重新生成即可。

在物联网中，一般不会出现，因为固定的监控等固定设备不会退出

监督

每个结点维护动态数组，记录信誉值。

发现消息不合法，广播，收到$F+1$个不合法消息，那么扣除信用

设定阈值，低于下限移除
如果系统参与结点不足以保证信息恢复，那么不移除

如果是主节点作恶，那么向其他诚实结点互相发送消息，然后共同选出新的主节点

分组编码的联盟链设计（WHAT）

委员会选取

创新点：选出委员会代表（Commitee）代表其他结点参与共识，选出委员会主节点、委员会从结点、非委员会结点
优势：避免所有结点都来参与编码、解码之中，造成网络通信量的浪费

组内的拜占庭结点肯超过PBFT容错的阈值
本方案要求拜占庭敌手控制此分组前完成共识的操作，否则重新选举CE

$cred_j=hash_{256}(视图号,公钥,作恶次数,消息摘要)$
计算$cred$最小的前n个作为委员会，最小的做主节点

计算cred计入了“作恶次数”，在一定程度上可以惩罚作恶结点；
消息摘要在发送的时候因为携带数据可能有差异，所以保证了选举的随机性

💡这种方案仍然有可能让低分者参与到委员会中

引入刚刚的信誉分机制

对信用分分级，高者可以作为主节点竞争者

中间评级参与到委员会的竞争中

低于阈值只能作为普通的非委员会结点

数据分片、编码、解码

分片&编码

均在委员会主节点中进行

对原始区块进行数据分片，$B(h)$分割为$r$片$\{B_1(h)、B_2(h)、…、B_r(h)\}$
对每一个一级分片$B_i(h)$切割为二级分片
对每个二级分片进行RS编码$(k,N)-RS$

与上一节不同，这里的$k$（最小使用多少块可以恢复分片数据）≠$N-2F$，而是这一组诚实结点的数量$f+1$

签名

均在委员会中进行

主节点广播编码结果
委员会成员对全部编码值签名，全网广播
委员会$M1、M2、\cdots、M_n$收到$F+1$个组内commit，达成共识
委员会主节点收到达成共识的消息，聚合二级签名$\sigma_{h,r,s}$

这里只需聚合委员会的签名(因为只有委员会代表非委员会结点参与共识)，相比聚合全部节省了很多的存储空间
委员会主节点需要同时帮助“非委员会结点”聚合签名；委员会从节点只需聚合自己的签名
主节点再将非委员结点要存储的信息告知给非委员会结点

消息解码

向组内发送decode消息，即可拿到所有二级分片

为什么不是全网发送decode消息，毕竟其他非委员会结点也存储了信息？
因为这里用的编码是$(k,N)-RS$编码，也就仅仅需要委员会的就足够了
如果委员会内部发生被控制的情况，再通过全网告知，全网也可以恢复数据，做一个备份。同时在这里减少了通信量

视图切换

为每一个委员会结点设定定时器（类似[[../../学习/区块链/Hotstuff相关的改进]]）超时触发视图切换

四个阶段

Viewchange 阶段

检测到超时，进入视图切换流程
< VIEWCHANGE, v + 1, p, ba, da, be, de, C, A, i >

v是视图号
p是最近的检查点编号
ba是分组最新已经共识的区块
- 如果一旦发现自己最新的待共识区块有问题，那么也可以及时补救
- 同样也为了防止篡改，只要大家对于上一个区块已经达成共识这一内容达成共识，那么前面的内容就无法被篡改了
be是当前待共识的区块
- 保证所有区块在“最新的共识区块”上保持共识
da、de相当于是ba、be的哈希
CA是证书，关于ba、be的

Election 阶段

一个结点收到$f+1$个消息后，即确认需要进行视图切换
< ELECTION, v + 1, ba, da, be, de, V >

V是新视图的证书

$f+1$可以看作一个共识的达成，即达成了需要重新选举委员会的共识

思考：如果有结点因为网络问题未收到消息，其他结点收到了怎么办？

如果未收到的是小部分结点，那么会在一定的时间内超时 （因为其他结点都还在选举委员会，未进行区块共识），因而发现自己脱离了共识体制

如果未收到的是大部分结点，那么后续共识过程也会因为参与共识的结点数目不足无法完成共识，造成再次重复选举

每个结点，按照相同的算法计算每个结点的积分$credit$

$credit_j=hash_{256}(v+1,da,de,PK_J,mal)$

$PK_J$是结点的公钥，$mal$表示作恶次数

选出委员会从结点和委员会主节点

$\begin{align} 委员会成员 &=MIN(\{credit_1,credit_2,\cdots,credit_N\},n) \\ \end{align}$

Ready 阶段

$委员会主结点=MIN(\{credit_1,credit_2,\cdots,credit_N\},1)$
委员会中选出主节点，委员会成员向主节点发出ready消息，等待主节点发送newview。
如果超时未收到——重新选举

Newveiw 阶段

收到$2f+1$个ready消息时

$2f+1$保证达成共识，因为要想达成共识必须满足${N-f}(正确结点)>f（错误结点）\Rightarrow N>2f$

向全网广播“已经切换到新视图了”，并发一个新的证书
< NEWVIEW, v + 1, da, de, C, A, V, R >

CA是关于区块共识情况（已经共识的区块和待共识的区块，即babe）的证书
V是视图的证书
R是主节点的证书
几个证书分别验证——
1. 区块的共识情况已经一致了
2. 我们已经切换了视图，当前视图号是v+1
3. 新的主节点已经选举

安全分析

超时设定：一轮（四个$\Delta$）

情形一：超时未共识，恶意和正确结点同时发生更换
- 正常结点和恶意结点均组内多播viewchange
- 每个结点收到了其他的viewchange，这时恶意结点选举恶意的结点作为委员会；正常结点正常选举，分别发送$election_{good}$、$election_{bad}$
- 此时会选出两个分组，正确委员会和错误委员会，分别发送$ready_{good}$、$ready_{bad}$
- 正确委员会广播newview，错误委员会会发现错误（发现$credit$函数计算值和哈希不匹配）因而放弃election
情形二：恶意结点恶人先告状，并不进行后续共识
- 恶意结点发送viewchange
- 恶意结点收到了足够消息，向恶意结点广播伪造的election；正确结点因为超时，进入重新选举
  
  这里的数据仅发送给恶意结点（多播），而不发送给正确结点，否则同情况一
- 正确结点全网广播正确的election；部分结点基于第二部错误的election发送ready
- 所有结点收到正确的election并丢弃正确的election
情形三：恶意结点恶人先告状，进行后续共识
- 恶意结点发送viewchange
- 恶意结点收到了足够消息，全网广播伪造的election；新的共识结果形成，告知全网
- 收到伪造election的选举错误的委员会，委员会发送ready选举错误的而主节点
- 所有结点均收到了新共识结果，共识结果与恶意节点的消息中的共识不一致，丢弃。

实验分析（HOW）

存储

（N-2F，N）-RS编码：分片更多，存储效率高
（f+1，N）-RS编码：分片少，存储效率较低

因为要保证选举出来的委员会的正常结点至少为$f+1$个，有部分正确结点未被选入委员会。因此无法保证分片效率
💡通过信用值来区分哪些可以进入委员会，尽量选择信用值高的委员会。可以一定程度上提高$f+1$的数量值，使得其编码效率进一步靠近第一种
全存储：存储效率极低

系统吞吐&平均时延

系统每单位时间所处理的总负载

因为加入了委员会的输出仅需要委员会组内进行组合即可，因此其输出效率高

基于编码的许可链

现存问题 (WHY:为什么需要改进)

传统方案

技术介绍

纠删码技术

分类

RS编码

范德蒙 RS 编码

柯西编码

RS编码的联盟链设计（WHAT）

核心思想

数据分片

分片数量的确定

数字签名

签名时间

验证&聚合签名

数据恢复

系统重初始化

新节点加入

我的想法💡

结点退出系统

退出后仍可解密

退出后无法解密

监督

分组编码的联盟链设计（WHAT）

委员会选取

数据分片、编码、解码

分片&编码

签名

消息解码

视图切换

四个阶段

Viewchange 阶段

Election 阶段

Ready 阶段

Newveiw 阶段

安全分析

实验分析（HOW）

存储

系统吞吐&平均时延

现存问题 (WHY:为什么需要改进)

传统方案

技术介绍

纠删码技术

分类

RS编码

范德蒙 RS 编码

柯西编码

RS编码的联盟链设计 （WHAT）

核心思想

数据分片

分片数量的确定

数字签名

签名时间

验证&聚合签名

数据恢复

系统重初始化

新节点加入

我的想法💡

结点退出系统

退出后仍可解密

退出后无法解密

监督

分组编码的联盟链设计 （WHAT）

委员会选取

数据分片、编码、解码

分片&编码

签名

消息解码

视图切换

四个阶段

Viewchange 阶段

Election 阶段

Ready 阶段

Newveiw 阶段

安全分析

实验分析（HOW）

存储

系统吞吐&平均时延

RS编码的联盟链设计（WHAT）

分组编码的联盟链设计（WHAT）