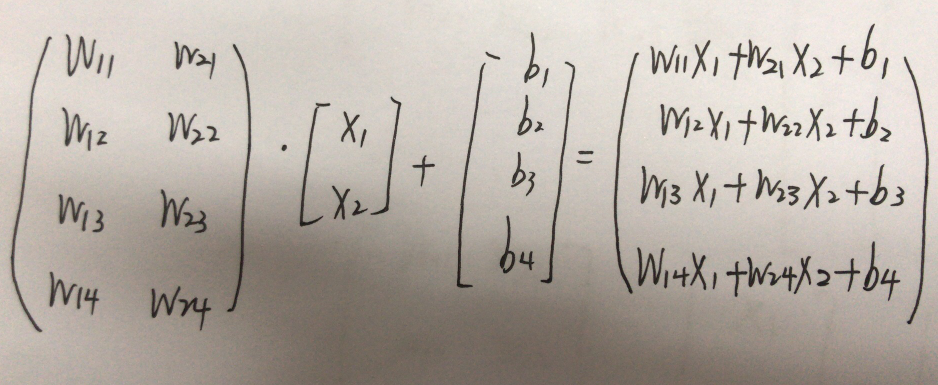神经网络入门
神经网络基础
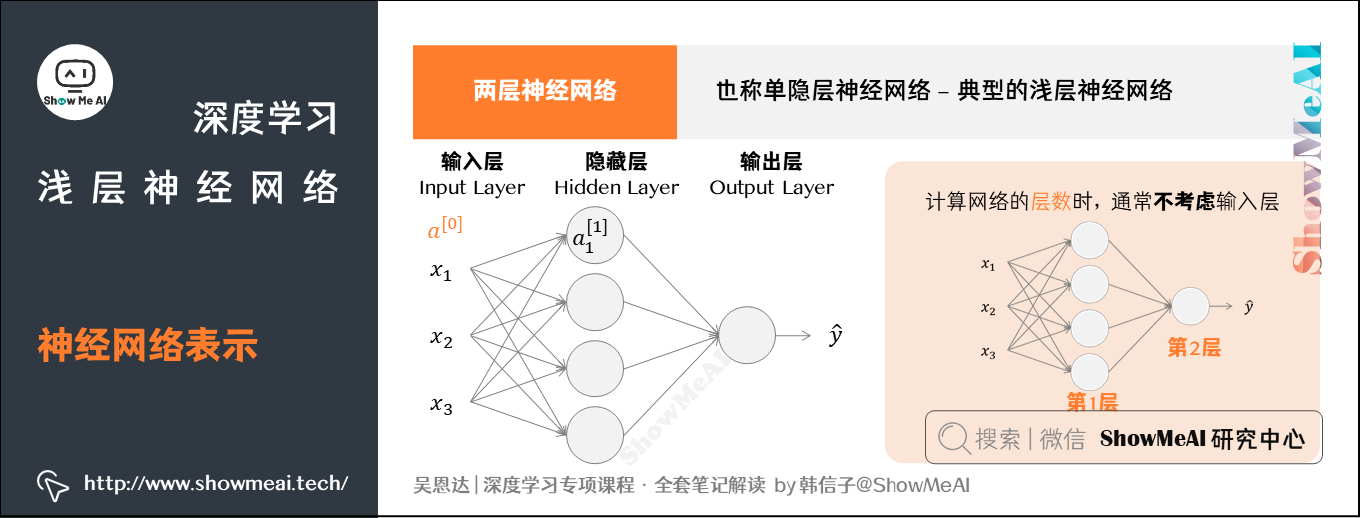
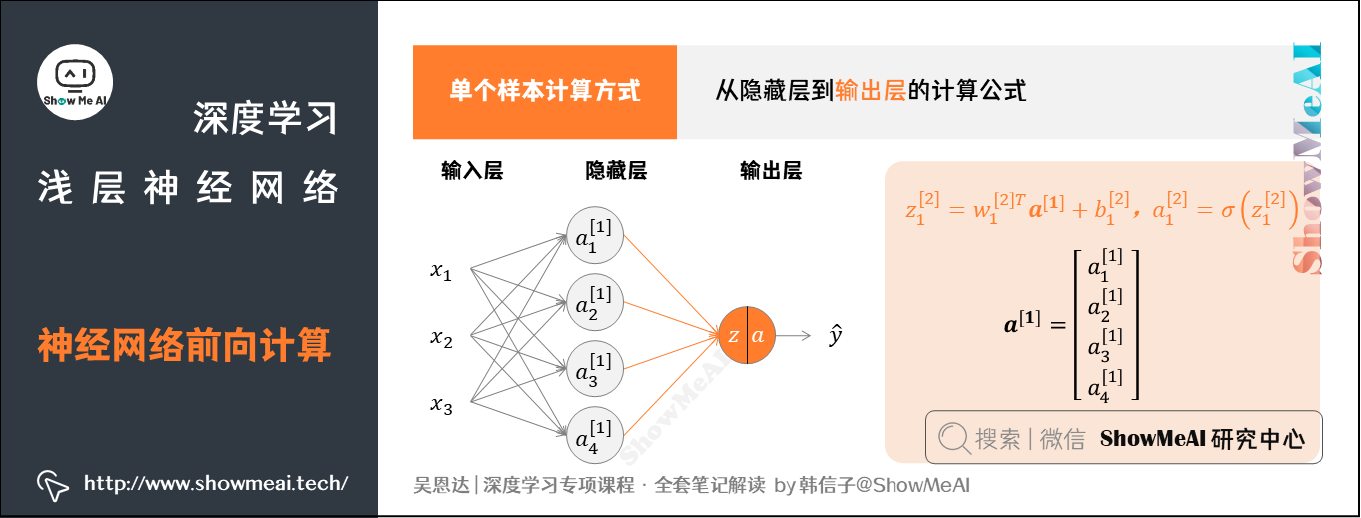
图示为两层神经网络,也可以称作单隐层神经网络 (a single hidden layer neural network) 。这就是典型的浅层 (shallow) 神经网络,结构上,从左到右,可以分成三层:
- 输入层 (input layer) :竖向堆叠起来的输入特征向量。
- 隐藏层 (hidden layer) :抽象的非线性的中间层。
- 输出层 (output layer) :输出预测值。
有一些约定俗成的符号表示,如下:
- 输入层的激活值为 $a^{[0]}$ ,隐藏层产生的激活值,记作 $a^{[1]}$ 。
- 隐藏层的第一个单元 (或者说节点) 就记作$a_1^{[1]}$ ,输出层同理。
- 隐藏层和输出层都是带有参数 $W$ 和$b$ 的,它们都使用上标[1]来表示是和第一个隐藏层有关,或者上标[2]来表示是和输出层有关。
我们记上标方括号 $[]$表示layer,记下标表示第几个神经元。
上标从0开始,下标从1开始
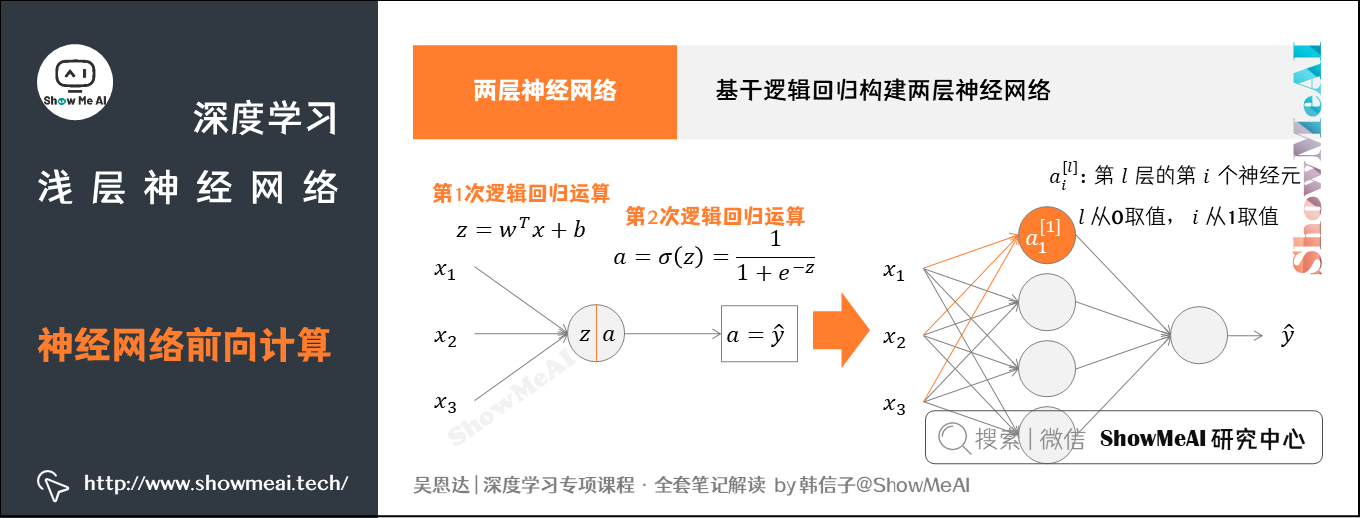
逻辑回归的前向传播计算可以分解成计算 $z$ 和 $a$ 的两部分。
- 计算 $z$:加权、偏执
- 计算 $a$:激活函数
整个的结构为
前向计算从前往后要做2次计算:
- 从输入层到隐藏层,对应一次逻辑回归运算。
- 从隐藏层到输出层,对应一次逻辑回归运算。
前馈神经网络
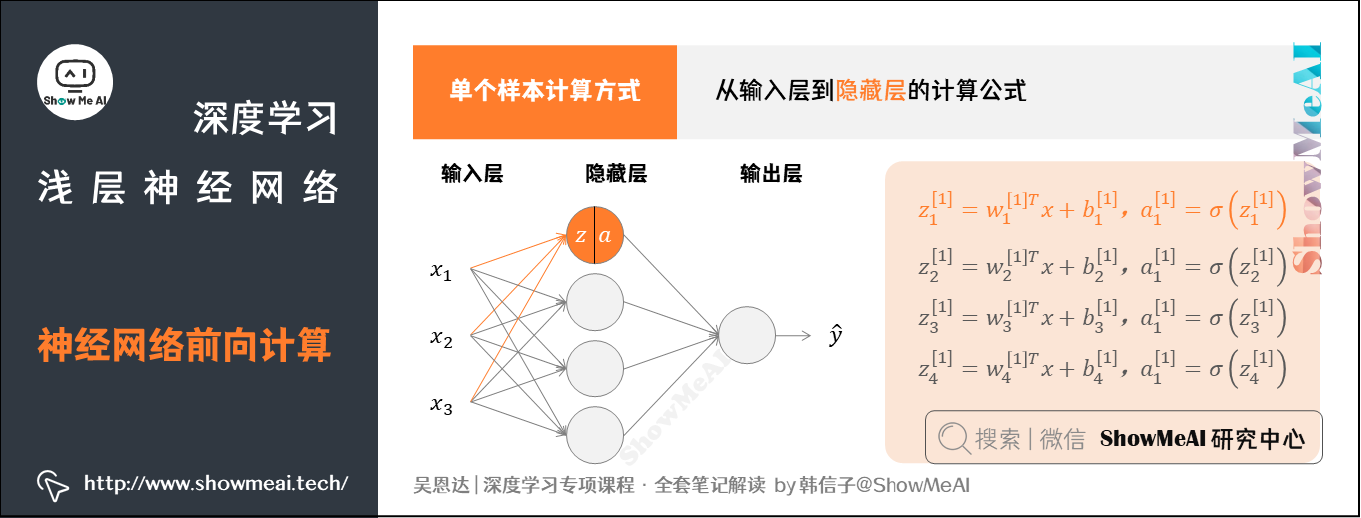
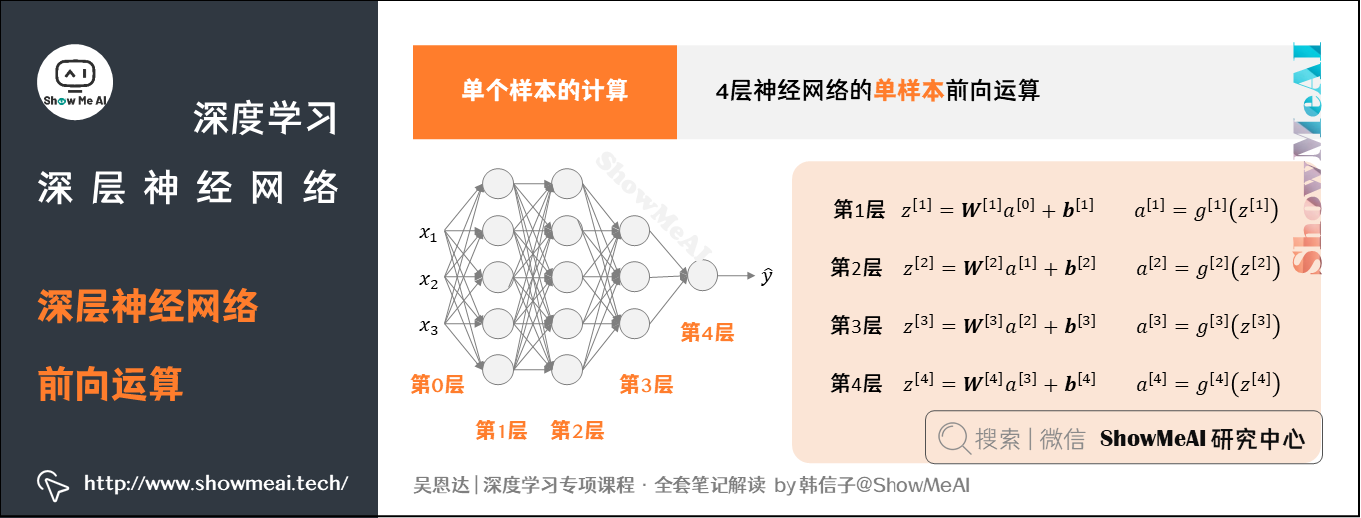
上述每个节点的计算都对应着一次逻辑运算的过程,分别由计算 $z$ 和 $a$ 的两部分。
- $z$:即一个线性计算的过程的得出
- $a$:即激活函数的结果得出.
值不断地向前传播,即前向计算
另外,我们想让输出结果变为概率,而不是一个值,那么就需要 正规化
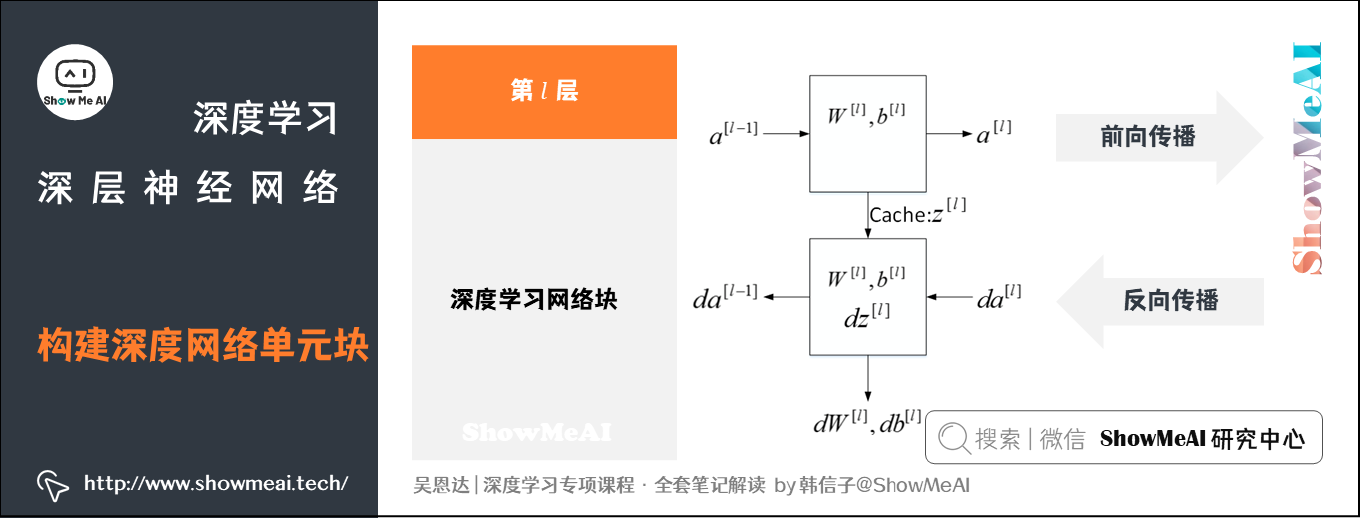
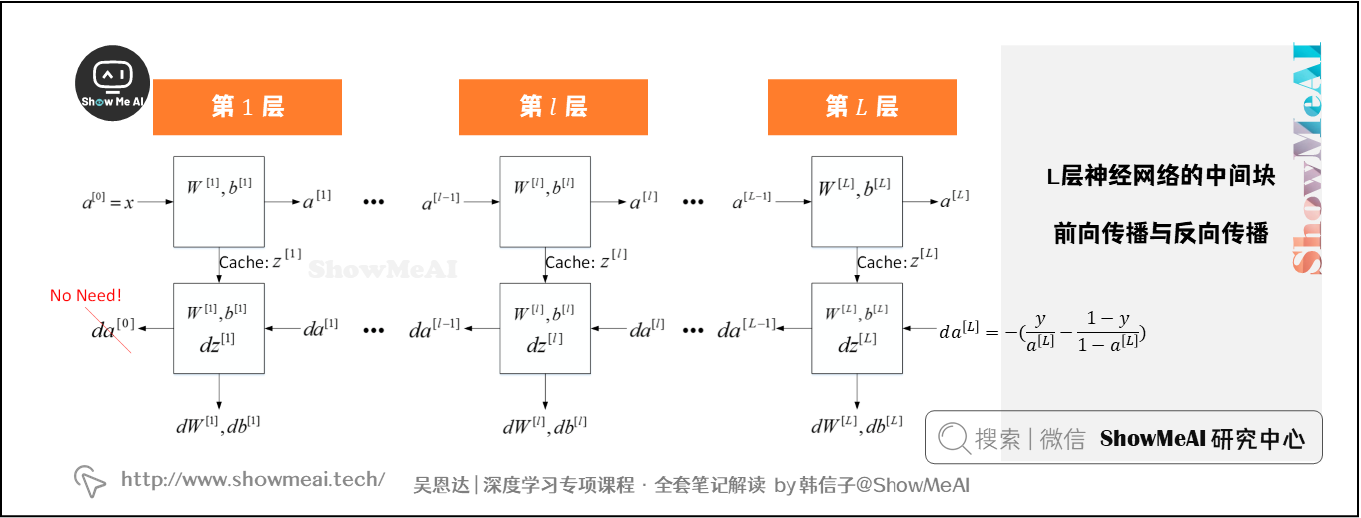
反向传播
反向来计算新的$w$值,使得其能很好的拟合.
反向传播就是一个参数优化的过程,优化对象就是网络中的所有W和b(因为其他所有参数都是确定的)。
以正则化项为$\frac{1}{2}W^2$为例子,求导后为$W$,那么可以写为(正则化惩罚项的系数值为reg) ——
分解模块
正规化Softmax
输出Y的值可能会是(3,1,0.1,0.5)这样的矩阵,诚然我们可以找到里边的最大值“3”,从而找到对应的分类为I,但是这并不直观。我们想让最终的输出为概率,也就是说可以生成像(90%,5%,2%,3%)这样的结果,这样做不仅可以找到最大概率的分类,而且可以知道各个分类计算的概率值。
此函数即Softmax函数,可以将多个标量映射为一个概率分布
BUT!实际应用中会存在一个问题,比如i的值等于1000时,$e^{1000}$在计算机中会变成无穷大的inf,后续计算将无法完成,所以程序中会对计算公式做一些修改,实际使用的公式为:
C为本组向量中的最大值
损失函数
就是计算$真实值-估计值$的差异,官话是 衡量模型输出与真实的标签之间的差距。$Loss=f(\hat{y},y)$
- 代价函数:描述的是总体样本\整个数据集的Loss的平均值 $Cost=\frac{1}{N}\sum f(\hat{y},y)$
- 目标函数:多了一个正则项(防止过拟合)$Obj=Cost+RT$
常见的损失函数
【方式1】MSE (均方误差, Mean Squared Error):输出与标签之差的平方的均值,常在回归任务中使用
【方式2】
Softmax正规化输出的结果是(90%,5%,3%,2%),真实的结果是(100%,0,0,0)。虽然输出的结果可以正确分类,但是与真实结果之间是有差距的,一个优秀的网络对结果的预测要无限接近于100%,为此,我们需要将Softmax输出结果的好坏程度做一个“量化”。
一种直观的解决方法,是用1减去Softmax输出的概率,比如1-90%=0.1。不过更为常用且巧妙的方法是,求对数的负数。
用90%举例,对数的负数就是:$-\log 0.9=0.046$。可以想见,概率越接近100%,该计算结果值越接近于0,说明结果越准确,该输出叫做“交叉熵损失(Cross Entropy Error)”。
CE(Cross Entropy,交叉熵) :交叉熵源自信息论,用于衡量两个分布的差异,常在分类任务中使用。
p是指真是分布,q是模型的分布,试图用q去逼近p。分布之间的距离是没有对应关系的。在给定 p 的情况下,如果 q 和 p 越接近,交叉熵越小;如果 q 和 p 越远,交叉熵就越大。
激活函数
使用线性激活函数和不使用激活函数、无论神经网络有多少层,输出都是输入的线性组合,与没有隐藏层效果相当
参数与超参数
- 神经网络中的参数就是我们熟悉的$W^{[l]}$ 和 $b^{[l]}$
- 神经网络的超参数是例如学习率 $\alpha$,训练迭代次数$N$,神经网络层数 $L$,各层神经元个数 $n^{[l]}$,激活函数 $g(z)$等。
优化器
优化器的作用是通过更新模型的参数来最小化损失函数
优化器的选择一般与损失函数的选择是独立的。优化器的目标是最小化损失函数,而不同类型的损失函数对应着不同的任务。
深度学习的实用层面
数据选择与模型评估
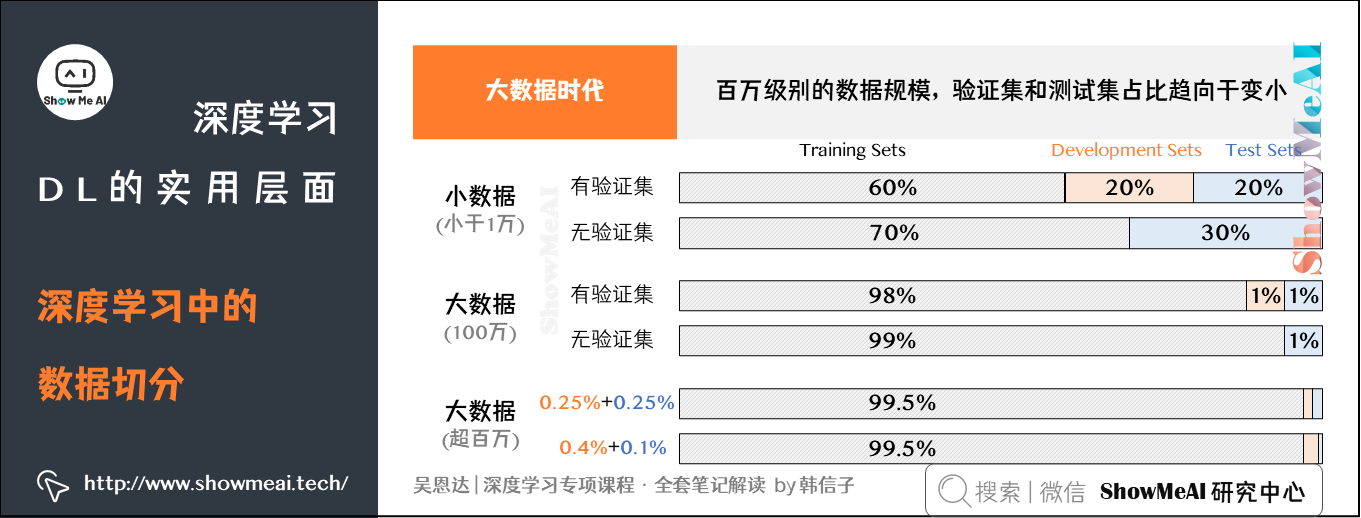
- 数据切分
- 训练集 (Training Sets) :用训练集对算法或模型进行训练过程。
- 验证集 ( (Development Sets) :利用验证集 (又称为简单交叉验证集,hold-out cross validation set) 进行交叉验证,选择出最好的模型。
- 测试集 (Test Sets) :最后利用测试集对模型进行测试,获取模型运行的无偏估计 (对学习方法进行评估) 。
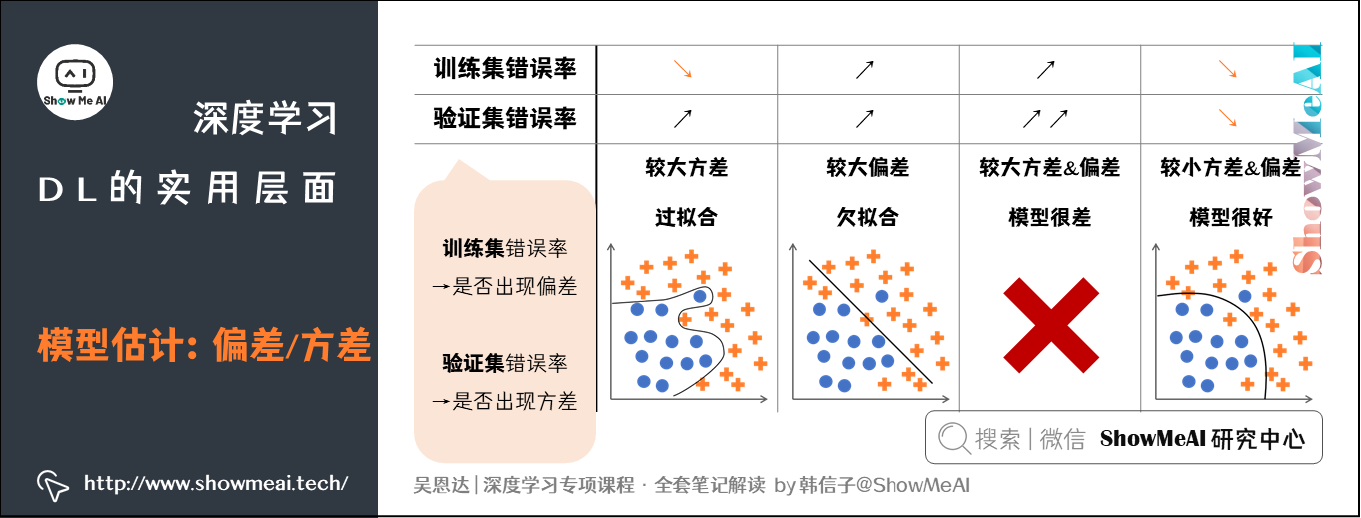
- 模型估计:是否过拟合
- 两个概念
- 偏差 (Bias) :度量了学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力。
- 方差 (Variance) :度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响。
训练集错误率体现了是否出现Bias (偏差) ,验证集 (和训练集差异) 错误率体现了是否出现Variance (方差)
- 解决思路
- 模型存在高偏差:扩大网络规模,如添加隐藏层或隐藏单元数目;寻找合适的网络架构,使用更大的NN结构;花费更长时间训练。
- 模型存在高方差:获取更多的数据;正则化 (Regularization) ;寻找更合适的网络结构。
正则化
蓝色圈的意思:若关注的维度越均衡,那么平方越小,惩罚越小.
手挫一个神经网络
1 | import numpy as np # 导入包 |
关于axis的维度
关于Softmax-with-Loss:Softmax-with-Loss指的就是Softmax和交叉熵损失的合称
从前面的层输入的是(a1, a2, a3),softmax层输出(y1, y2, y3)。此外,教师标签是(t1, t2, t3),Cross Entropy Error层输出损失L。
所谓教师标签,就是表示是否分类正确的标签,比如正确分类应该是第一行的结果时,(t1, t2, t3)就是(1,0,0)。
从上图可以看出,Softmax-with-Loss的反向传播的结果为(y1 − t1, y2 − t2, y3 − t3)。
参考文献
[1] https://zhuanlan.zhihu.com/p/635438713
[2] https://zhuanlan.zhihu.com/p/66534632