为什么突然写数据结构的,因为算法的(重温算法(基础知识) )实在写不下了
数组 前缀和与差分 前缀和 一维前缀和 前缀和指一个数组的某下标之前 的所有数组元素的和(包含其自身) 。前缀和分为一维前缀和,以及二维前缀和。前缀和是一种重要的预处理 ,能够降低算法的时间复杂度 。可以快速地求出某一段的和。
【问题】输入一个长度为n的整数序列。接下来再输入m个询问,每个询问输入一对l, r。对于每个询问,输出原序列中从第l个数到第r个数的和。
我们很容易想出暴力解法,遍历区间求和。这样的时间复杂度为O(n * m)nmO(n + m)
【做法】预处理 ,定义一个sum[]数组,sum[i]代表a数组中前i个数的和。
1 2 3 4 5 6 const int N = 1e5 + 10 ;int sum[N], a[N]; for (int i = 1 ;i <= n; i++){ sum[i] = sum[i - 1 ] + a[i]; }
对于每次查询,只需执行sum[r] - sum[l - 1] ,时间复杂度为O(1)
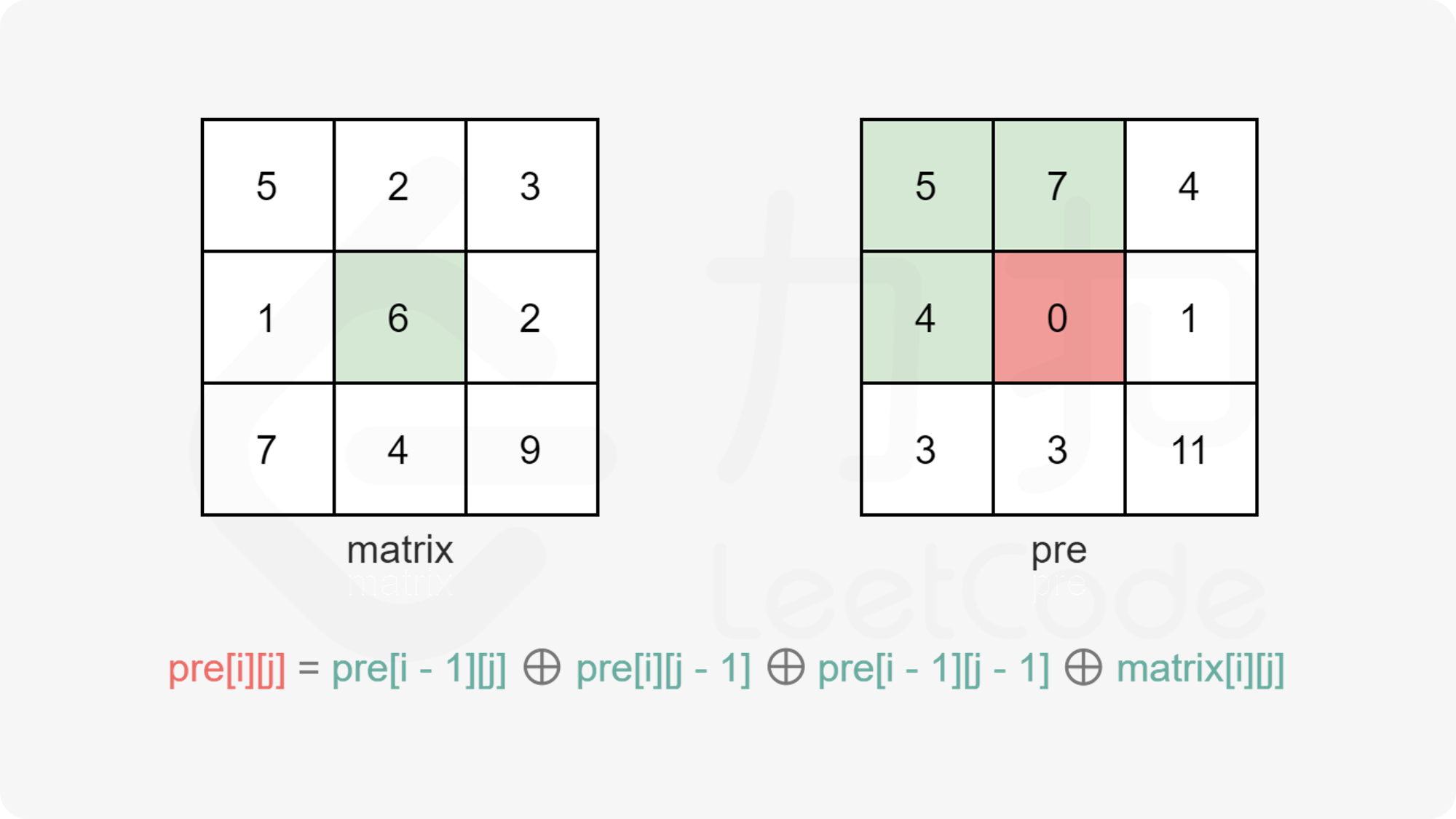
二维前缀和 和一维前缀和一样,我们需要构造一个前缀和数组s[i][j]。利用前缀和的思想:我们需要通过前面已知的前缀和来推出后面未知的前缀和。
从图中我们很容易看出,整个外围蓝色矩形面积s[i][j] = 绿色面积s[i - 1][j] + 紫色面积s[i][j - 1] - 重复加的红色的面积s[i - 1][j - 1] + 小方块的面积a[i][j] ; 因此得出二维前缀和预处理公式:
1 s[i][j] = s[i - 1 ][j] + s[i][j - 1 ] + a[i] [j] - s[i - 1 ][j - 1 ]
子矩阵的和1 2 3 4 matrixSum (int x1,int y1,int x2,int y2){}return s[x2][y2]-s[x2][y1-1 ]-s[x1-1 ][y2]+s[x1-1 ][y1-1 ];}
异或前缀和 可以使用「前缀和」这一技巧对按位异或运算的结果进行维护
$pre(i,j)=pre(i−1,j)⊕pre(i,j−1)⊕pre(i−1,j−1)⊕matrix(i,j)$
当我们将$\textit{pre}(i-1, j)$和$\textit{pre}(i, j-1)$进行按位异或运算后,由于对一个数 x 异或两次 y,结果仍然为 x 本身,即:$x \oplus y \oplus y = x$
因此 $pre(i−1,j−1)$对应区域的按位异或结果被抵消,我们需要将其补上,并对位置 $(i,j)$ 的元素进行按位异或运算,这样就得到了$pre(i,j)$。
差分 所谓差分可以理解为前缀和的逆运算 ,就是将数列中每一项分别与前一项做差。
差分数组: a[1], a[2], a[3]...... a[n];b[1], b[2], b[3]...... b[i];a[i] = b[1] + b[2] + b[3] + ...... + b[i]a数组是b数组的前缀和数组 ,反过来我们把b数组叫做a数组的差分数组 。
如何构造差分数组?
差分数组的性质:
1.对差分数组进行前缀和,就可以的到原数组
原数组
a1
a2
a3
a4
差分
a1
a2-a1
a3-a2
a4-a3
差分前缀和
a1
a2
a3
a4
2.要对数组区间[ l, r ]的数据都加上m 时,我们只需要对差分数组进行操作即可
即 L到前一个元素的距离+c,R到后一个元素的距离-c
Text
递推式:b[i][j]=a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]
改变——1 2 3 4 b[x1][y1] += c ; 让整个a数组中蓝色矩形面积的元素都加上了c。 b[x1,][y2 + 1] -= c ; 让整个a数组中绿色矩形面积的元素再减去c,使其内元素不发生改变。 b[x2 + 1][y1] -= c ; 让整个a数组中紫色矩形面积的元素再减去c,使其内元素不发生改变。 b[x2 + 1][y2 + 1] += c ; 让整个a数组中红色矩形面积的元素再加上c,红色内的相当于被减了两次,再加上一次c,才能使其恢复。
例题:差分矩阵 x1, y1, x2, y2, c,其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。
输入格式
第一行包含整数n, m, q。
接下来n行,每行包含m个整数,表示整数矩阵。
接下来q行,每行包含5个整数x1, y1, x2, y2, c,表示一个操作。
输出格式
共 n 行,每行 m 个整数,表示所有操作进行完毕后的最终矩阵。注意是如何构建差分数组和得到新数组的!
hl:"构建差分数组",前缀和,注意这里是往后看 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 #include <iostream> #include <cstdio> using namespace std;const int N = 1e3 + 10 ;int a[N][N], b[N][N];void insert (int x1, int y1, int x2, int y2, int c) b[x1][y1] += c; b[x2 + 1 ][y1] -= c; b[x1][y2 + 1 ] -= c; b[x2 + 1 ][y2 + 1 ] += c; } int main () int n, m, q; cin >> n >> m >> q; for (int i = 1 ; i <= n; i++) for (int j = 1 ; j <= m; j++) cin >> a[i][j]; for (int i = 1 ; i <= n; i++) { for (int j = 1 ; j <= m; j++) { insert (i, j, i, j, a[i][j]); } } while (q--) { int x1, y1, x2, y2, c; cin >> x1 >> y1 >> x2 >> y2 >> c; insert (x1, y1, x2, y2, c); } for (int i = 1 ; i <= n; i++) { for (int j = 1 ; j <= m; j++) { b[i][j] += b[i - 1 ][j] + b[i][j - 1 ] - b[i - 1 ][j - 1 ]; } } for (int i = 1 ; i <= n; i++) { for (int j = 1 ; j <= m; j++) { printf ("%d " , b[i][j]); } printf ("\n" ); } return 0 ; }
尺取法 尺取法通常是指对数组保存一对下标(起点,终点),然后根据实际情况交替推进两个端点直到得出答案的方法
在一个不断变化和移动的区间内进行统计,符合尺取法的特点
给定长度为n的数列整数$a_0,a_1,…,a_N$以及整数S。求出总和不小于S的连续子序列的最小长度。如果解不存在,则输出0。
尺取法可以表示为下面的过程
即,主要步骤为:
初始化时:左右指针都在0
只要当Sum<S, 那么右指针一直自增
Sum>=S时候终止自增,长度存入ans里面(后续比较ans取最小)
尺子定型了,Sum中减去最开头那个,然后左指针自增,重复回到第二步骤
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 void solve () int res=n+1 ; int s=0 ,t=0 ,sum=0 ; for (;;) { while (t<n&&sum<S) { sum+=a[t++]; } if (sum<S) break ; res=min (res,t-s); sum-=a[s++]; } if (res>n) res=0 ; cout<<res; }
线段树与树状数组 树状数组 先输入一个长度为n的数组,然后我们有如下两种操作:
输入一个数m,输出数组中下标1~m的前缀和
对某个指定下标的数进行值的修改
前缀和的效果就不行了,因为经过1.的时候必须更新前缀和。于n 次操作,时间复杂度就达到了O(n^2)和O(n),这样的方法就显得不适用了。
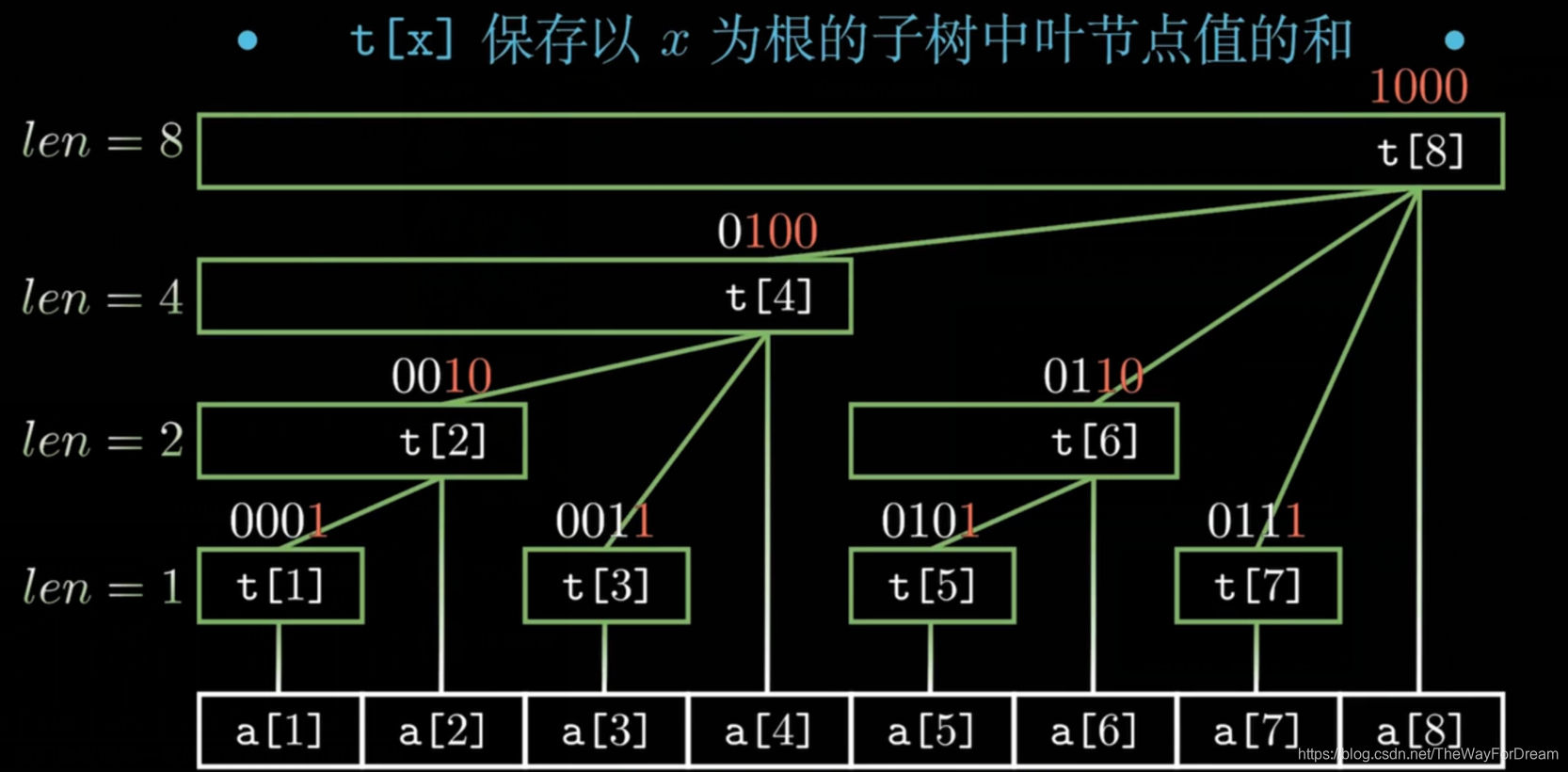
我们引入树状数组——如图,对于一个长度为n的数组,A数组存放的是数组的初始值,引入一个辅助数组C;
C1 = A1
我们称C[i]的值为下标为i的数所管辖的数的和。下标为i的数所管辖的元素的个数为$2^k$个(k为i的二进制的末尾0的个数)
i = 8 = 1000,末尾3个0,故k = 3,所管辖的个数为$2^3=8$,C8是8个数的和;i = 5 = 0101,末尾没有0,故k = 0,所管辖的个数为$2^0=1$,C5是一个数的和;
[补充]如何计算一个非负整数n在二进制下的最低为1及其后面的0构成的数?
所以lowbit(x) = x&(-x)
单点修改,区间查询 我们在单点修改 的同时,更新父节点就变得尤为简单,,例如我们对a[1]+k,那么祖先节点t[1],t[2],t[4],t[8]都需要+k更新(因为t[]表示前缀和),此时我们就可以用lowbit操作实现.
1 2 3 4 5 6 int add_dandian (int x,int k) for (int i=x;i<=n;i+=lowbit (i)) t[i]+=k; }
修改完成,如何进行区间查询?我们需要查询前7项的区间和sum[7]
sum[7]=t[7]+t[6]+t[4] ,我们进一步发现,6=7-lowbit(7),4=6-lowbit(6),所以我们可以通过不断的-lowbit操作来实现求和
1 2 3 4 5 6 7 8 int ask (x) int sum = 0 ; for (int i=x;i;i-=lowbit (i)){ sum+=t[i]; } return sum; }
这只能求区间[ 1 , x ] 的区间和,那么如何求 [ L , R ] 的区间和呢? [1,x]的区间和,那么如何求[L,R]的区间和呢?[1,x]的区间和,那么如何求[L,R]的区间和呢?,这时候利用前缀和相减的性质就可以了——$[L,R]=[1,R]−[1,L−1]$
1 2 3 4 5 6 7 8 9 10 int search (int L,int R) int ans = 0 ; for (int i=L-1 ;i;i-=lowbit (i)) ans-=t[i]; for (int i=R;i;i-=lowbit (i)) ans+=t[i]; return 0 ; }
区间修改,单点查询 对于这一类操作,我们需要构造出原数组的差分数组b ,然后用树状数组维护b数组即可
对于区间修改的话,我们只需要对差分数组进行操作即可,例如对区间[L,R]+k,那么我们只需要更新差分数组add(L,k),add(R+1,-k)
对于单点查询操作,求出b数组的前缀和即可,因为a[x]=差分数组b[1]+b[2]+…+b[x]的前缀和,这是差分数组的性质之一.
1 2 3 4 5 6 7 ll ask (int pos) ll ans=0 ; for (int i=pos;i;i-=lowbit (i)) ans+=c[i]; return ans; }
线段树 线段-区间-树
建树规则
用分治法自顶向下建立,每次分治,左右子树各一半。
每个节点都表示一个“线段”区间,非叶子节点包含多个元素,叶子节点只包含一个元素。
除了最后一层,其他层都是满的。
l=r,说明这是一个叶子节点。
l<r,说明他有两个子节点,左儿子[l,m],右儿子[mid+1,r],其中m=(l+r)/2;
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 int a[n];int sum[n*4 ];void push (int o) sum[o]=sum[o*2 ]+sum[o*2 +1 ]; } void build (int l,int r,int o) if (l==r) { sum[o]=a[l]; } else { int mid=(l+r)/2 ; build (l,mid,o*2 ); build (mid+1 ,r,o*2 +1 ); push (o); } }
单点修改:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 void updata (int p,int l,int r,int o,int k) if (l==r) { a[o]+=k; sum[o]+=k; } else { int mid=(l+r)/2 ; if (p<=mid) { updata (p,l,mid,o*2 ,k); } else { updata (p,mid+1 ,r,o*2 +1 ,k); } push (o); } }
区间修改:
我们引进一个新玩意:lazy-tag。tag[i]记录了区间i的修改,这样就不用一个一个的再去修改去区间的内的每个元素了。
当我们进行修改时,先只对这个线段区间上进行整体上的修改 ,其内部每个元素的值先不修改 。只有当查找到的区间不包含在给定的区间时(即lR时),才把变化值传给下一层的子区间,即修改内部元素。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 void down (int l,int r,int o) if (tag[o]) { int mid=(l+r)/2 ; tag[o*2 ]+=tag[o]; tag[o*2 +1 ]+=tag[o]; sum[o*2 ]+=tag[o]*(mid-l+1 ); sum[o*2 +1 ]+=tag[o]*(r-mid); tag[o]=0 ; } } void updata (int L,int R,int l,int r,int o,int k) if (l>=L&&r<=R) { tag[o]+=k; sum[o]+=k*(r-l+1 ); } else { down (l,r,o); int mid=(l+r)/2 ; if (L<=mid) { updata (L,R,l,mid,o*2 ,k); } if (mid<R) { updata (L,R,mid+1 ,r,o*2 +1 ,k); } push (o); } }
第二个else不太好理解哈,
我希望[1,2]都加1,根据我们的代码:
(1)从整棵树的根节点开始,递归至左子树[1,2],被修改区间[1,2]完全覆盖,于是sum[2]+=1*(2-1+1)=3,tag[o]+=1=1
这样以来,节点2([1,2]区间)的和就成了5,但节点4和5的值还没修改。
lazy-tag正如它的名字一样——懒标记(延时标记),他不会立刻去一次性的把被修改区间的值全修改掉,而是从一个符合条件的节点开始,当需要的时候他才会去修改被标记节点下面的值。
传递函数down()是处理lazy-tag的一个技巧。在进行多次区间修改时,一个节点需要记录多个区间修改,而这些区间修改往往有冲突。例如,做两次区间修改,一次是[4,9],一次是[5,8],它们都会影响5:[4,5]这个节点。第1次修改区间[4,9]覆盖了节点5,用tag[5]做了记录;而第⒉次修改区间[5,8]不能覆盖节点5,需要再向下搜索到节点11:[5,5],从而破坏了tag[5],此时原tag[5]记录的区间统一修改就不得不向它的子节点传递和执行了,传递后tag[5]失去了作用,需要清空。所以,lazy-tag 的主要操作是解决多次区间修改,用down()函数完成。首先检查节点p的tag[p],如果有值,说明前面做区间修改时给p打了tag标记,接下来就把 tag[p]传给左右子树,然后把 tag[p]清零。
完全覆盖
部分覆盖
当mid>=L也就是L与左子树有交集时,我们去递归左子树
TBD 真心看不懂
其他线性结构 栈 单调栈 当题目出现「找到最近一个(左侧/右侧)比其大的元素」的字眼时,自然会想到「单调栈」。大多数情况用于求解出的结果明显的呈现出V或者^形式的问题 。其意思是栈内的元素是单调的。根据栈内元素的单调性的不同,可以分为:
单调递增栈:栈内元素是单调递增的栈。
单调递减栈:栈内元素是单调递减的栈。
完全单调栈 1 2 3 4 5 6 7 8 9 10 11 遍历下面的数组元素维护一个递减栈: arrs = [2,4,3,6,5,7,1] stack = [] (1).栈空2入栈 stack = [2] (2).4>2 2出栈,4入栈 stack = [4] (3).3<4 3入栈 stack = [4,3] (4) stack = [6] (5) stack = [6,5] (6) stack = [7] (7) stack = [7,1]
图解 以单调递增栈为例子——
即一旦找到比栈顶更大的,就弹出来
最终——
例题 【下一个更大元素 I 】x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。没有重复元素 的数组 nums1 和 nums2 ,下标从 0 开始计数,其中nums1 是 nums2 的子集。
返回一个长度为 nums1.length 的数组 ans 作为答案,满足 ans[i] 是如上所述的 下一个更大元素 。
示例 1:
4 ,用加粗斜体标识,nums2 = [1,3,4 ,2]。不存在下一个更大元素,所以答案是 -1 。
1 ,用加粗斜体标识,nums2 = [ 1 ,3,4,2]。下一个更大元素是 3 。
2 ,用加粗斜体标识,nums2 = [1,3,4,2 ]。不存在下一个更大元素,所以答案是 -1 。
2 ,用加粗斜体标识,nums2 = [1,2 ,3,4]。下一个更大元素是 3 。
4 ,用加粗斜体标识,nums2 = [1,2,3,4 ]。不存在下一个更大元素,所以答案是 -1 。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 class Solution {public : vector<int > nextGreaterElement (vector<int >& nums1, vector<int >& nums2) { unordered_map<int ,int > hashmap; stack<int > st; for (int i = nums2. size () - 1 ; i >= 0 ; --i) { int num = nums2[i]; while (!st.empty () && num >= st.top ()) { st.pop (); } hashmap[num] = st.empty () ? -1 : st.top (); st.push (num); } vector<int > res (nums1. size()) ; for (int i = 0 ; i < nums1. size (); ++i) { res[i] = hashmap[nums1[i]]; } return res; } };
为什么是从后向前遍历:因为求得是对应元素 下一个 得更大元素。下一个靠右,所以需要先遍历右边得更大 得
前缀和+单调栈 普通前缀和 前缀和是一个保证能够递增的数据结构,我们可以与之和单调栈结合
和至少为k的连续子数组
子数组 是数组中 连续 的一部分。
示例 1:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 class Solution {public : int shortestSubarray (vector<int > &nums, int k) int n = nums.size (), ans = n + 1 ; long s[n + 1 ]; s[0 ] = 0L ; for (int i = 0 ; i < n; ++i) s[i + 1 ] = s[i] + nums[i]; deque<int > q; for (int i = 0 ; i <= n; ++i) { long cur_s = s[i]; while (!q.empty () && cur_s - s[q.front ()] >= k) { ans = min (ans, i - q.front ()); q.pop_front (); } while (!q.empty () && s[q.back ()] >= cur_s) q.pop_back (); q.push_back (i); } return ans > n ? -1 : ans; } };
如果遇到与栈的性质相反的,需要弹栈,看图2
所以:单调栈的核心在于——及时移除无用数据,保证队列/栈的有序性 。
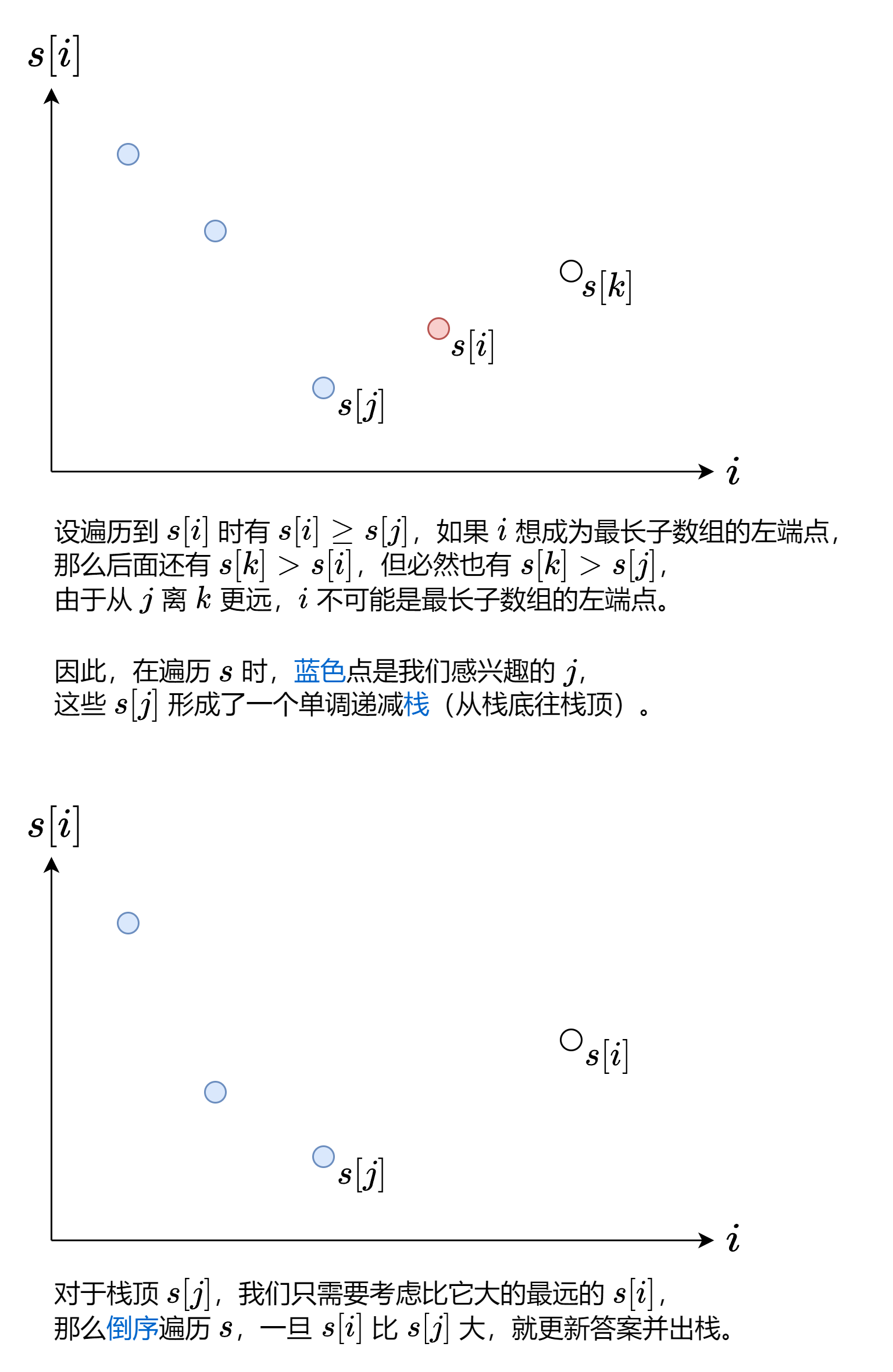
单调栈求跨度 核心思路:遍历一遍,生成一个单调递减(增)栈,保存从左到右出现的最小(大)值的下标
普通跨度 参考力扣-最大宽度坡
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 class Solution {public : int maxWidthRamp (vector<int >& nums) int len = nums.size (); int ans = 0 ; stack<int > s; for (int i = 0 ; i < len; i++) { if (s.empty () || nums[s.top ()] > nums[i]) { s.push (i); } } int res = 0 ; for (int j = len - 1 ; j >= 0 ; j--) { while (!s.empty () && nums[s.top ()] <= nums[j]) { int pos = s.top (); s.pop (); res = max (res, j - pos); } } return res; } };
变式前缀和+最长最宽 如果要形成V型或者类似于V的,可以先求出↘的最低端,然后找到↗最大点1124. 表现良好的最长时间段
示例 1:
先把问题转换到我们熟悉的东西上。
「劳累天数大于不劳累天数」等价于「劳累天数减去不劳累天数大于 000」。
那么把劳累的一天视作 nums[i]=1,不劳累的一天视作 nums[i]=−1,则问题变为:
计算 nums的最长子数组,其元素和大于 0。
即:j<i 且 s[j]<s[i],最大化 i−j 的值。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 class Solution {public : int longestWPI (vector<int > &hours) int n = hours.size (), ans = 0 , s[n + 1 ]; stack<int > st; st.push (s[0 ] = 0 ); for (int j = 1 ; j <= n; ++j) { s[j] = s[j - 1 ] + (hours[j - 1 ] > 8 ? 1 : -1 ); if (s[j] < s[st.top ()]) st.push (j); } for (int i = n; i; --i) while (!st.empty () && s[i] > s[st.top ()]) { ans = max (ans, i - st.top ()); st.pop (); } return ans; } };
字符串 KMP Everything is a state machine
我们可以以状态机的形式重新审视整个匹配过程
要匹配的过程形成了一种链式 结构,每个结点都是当前匹配的状态,如果再当前结点的下一个结点不同,我们走的路径也不同
因此:要确定状态转移的行为,得明确两个变量,一个是当前的匹配状态,另一个是遇到的字符 ;确定了这两个变量后,就可以知道这个情况下应该转移到哪个状态。
1 2 3 4 5 6 7 8 9 10 11 12 dp[j][c] = next 0 <= j < M,代表当前的状态 0 <= c < 256,代表遇到的字符(ASCII 码) 0 <= next <= M,代表下一个状态 dp[4]['A'] = 3 表示: 当前是状态 4,如果遇到字符 A, pat 应该转移到状态 3 dp[1]['B'] = 2 表示: 当前是状态 1,如果遇到字符 B, pat 应该转移到状态 2
核心流程是
1 2 3 4 5 6 7 8 9 10 11 12 13 14 int M = pat.length (); int N = txt.length (); int j = 0 ; for (int i = 0 ; i < N; i++) { j = dp[j][txt.charAt (i)]; if (j == M) return i - M + 1 ; } return -1 ;
现在的首要目标就是构造dp,很简单
1 2 3 for 0 <= j < M: # 状态 for 0 <= c < 256: # 字符 dp[j][c] = next
这个 next 状态应该怎么求呢?
显然,如果遇到的字符 c 和 pat[j] 匹配的话 ,状态就应该向前推进一个,也就是说 next = j + 1,我们不妨称这种情况为状态推进
如果字符 c 和 pat[j] 不匹配的话 ,状态就要回退(或者原地不动),我们不妨称这种情况为状态重启
所谓影子状态,就是和当前状态具有相同的前缀 。比如下面这种情况:当前状态 j = 4,其影子状态为 X = 2,它们都有相同的前缀 “AB”。因为状态 X 和状态 j 存在相同的前缀,所以当状态 j 准备进行状态重启的时候(遇到的字符 c 和 pat[j] 不匹配),可以通过 X 的状态转移图来获得最近的重启位置 。
如果状态 j 遇到一个字符 “A”,应该转移到哪里呢?首先只有遇到 “C” 才能推进状态,遇到 “A” 显然只能进行状态重启。状态 j 会把这个字符委托给状态 X 处理,也就是 dp[j]['A'] = dp[X]['A'] :那么 j 就可以去问问和自己具有相同前缀的 X,如果 X 遇见 “A” 可以进行「状态推进」,那就转移过去,因为这样回退最少。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 public KMP (String pat) this .pat = pat; int M = pat.length (); dp = new int [M][256 ]; dp[0 ][pat.charAt (0 )] = 1 ; int X = 0 ; for (int j = 1 ; j < M; j++) { for (int c = 0 ; c < 256 ; c++) { if (pat.charAt (j) == c) dp[j][c] = j + 1 ; else dp[j][c] = dp[X][c]; } X = dp[X][pat.charAt (j)]; }
参考
next数组
例:‘ababa’
‘a’的前缀和后缀都为空集,最长相等前后缀长度为0 。
‘ab’的前缀为{a},后缀为{b},最长相等前后缀长度为0 。
……
‘ababa’的前缀:{a,ab,aba,abab},后缀:{a,ba,aba,baba},最长相等前后缀长度为3。
子串跳过最后一个比对成功的next数组 ,j到达子串末尾匹配成功
特点:主串指针永不回退 !
伪代码
代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 vector<int > commpute_next (string pattern) { vector<int >next (pattern.size () + 1 , 0 ); next[0 ] = -1 ; for (int i = 2 ; i < next.size (); ++i) { for (int j = 1 ; j < i; ++j) { if (pattern.substr (0 , j) == pattern.substr (i - j, j)) { next[i] = j; } } } return next; } int kmp (string str,string pattern) vector<int > next = commpute_next (pattern); int i = 0 ; int j = 0 ; while (i < str.size ()) { if (str[i] != pattern[j]) { j = next[j]; if (j == -1 ) { i++; j = 0 ; } }else { i++; j++; if (j == pattern.size ()) { return (int ) (i - pattern.size ()); } } } return -1 ; }
参考2
compute_next可以更高效,请参考文章 实现
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 vector<int > commpute_next (string pattern) { vector<int >next (pattern.size () + 1 , 0 ); next[0 ] = -1 ; next[1 ] = 0 ; int i = 2 ; int k = 0 ; while (i < next.size ()) { if (pattern[i - 1 ] == pattern[k]) { next[i] = k + 1 ; k = next[i]; ++i; } else if (k == 0 ){ next[i] = 0 ; ++i; } else { k = next[k]; } } return next; } int kmp (string str,string pattern) vector<int > next = commpute_next (pattern); int i = 0 ; int j = 0 ; while (i < str.size ()) { if (str[i] != pattern[j]) { j = next[j]; if (j == -1 ) { i++; j = 0 ; } }else { i++; j++; if (j == pattern.size ()) { return (int ) (i - pattern.size ()); } } } return -1 ; }
或者
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 void getNext (char * s,int len) { next[0 ] = 0 ; int k = 0 ; int i = 1 ; while (i < len){ if (s[i] == s[k]){ next[i] = k+1 ; k++; i++ }else { if (k > 0 )k = next[k-1 ]; else { next[i++] = k; } } } } int kmp (char *T, char * S) { int len_T = strlen (T); int len_S = strlen (S); for (int i = 0 ,j = 0 ;i<len_T;i++){ while (j > 0 && T[i] != S[j]) j = next[j-1 ]; if (T[i] == S[j])j++; if (j == len_S) return i-len_S+1 ; } return -1 ; } int kmp (char *T, char * S) { int sum = 0 ; int len_T = strlen (T); int len_S = strlen (S); for (int i = 0 ,j = 0 ;i<len_T;i++){ while (j > 0 && T[i] != S[j]) j = next[j-1 ]; if (T[i] == S[j])j++; if (j == len_S){ sum++; j = next[j-1 ]; } } return sum; }
树 前缀树 并查集 (实际是数组,但借助树的思想)
参考文章
用于处理一些元素分组 的问题。它主要用于处理一些不交集的合并及查询 问题 (不交集指的是一系列没有重复元素的集合。) 。在计算机科学中,并查集算法常常用于解决连通性问题,如判断图中的两个节点是否属于同一个连通分量,或者判断一个无向图是否是连通图等。解决一些父节点与子节点 之间的关系,重要的就是查和并
简单来说,并查集就是用来处理集合的合并和集合的查询。
并查集中的「集」指的就是我们初中所学的集合概念 ,在这里指的是不相交的集合,即一系列没有重复元素的集合。
并查集中的「并」指的就是集合的并集操作 ,将两个集合合并之后就变成一个集合。合并操作如下所示:
{1, 3, 5, 7} ∪ {2, 4, 6, 8} = {1, 2, 3, 4, 5, 6, 7, 8}
「并查集」结构所支持的操作接口:
合并 union(x, y) :将集合 x 和集合 y 合并成一个集合。查找 find(x):查找元素 x 属于哪个集合。查找 is_connected(x, y) :查询元素 x 和 y 是否在同一个集合中。
【步骤】初始化 。定义一维数组int s[],s[i]是结点i的并查集,开始的时候,还没有处理点与点之间的朋友关系,所以每个点属于独立的集,直接初始化s[i] = i,例如结点1的集s[1] = 1。
(2)合并 ,例如加入第一个朋友关系(1, 2)。在并查集s中,把结点1合并到结点2,也就是把结点1的集1改成结点2的集2,set[1] = set[2] = 2。此时5人的关系用4个集表示,其中set[2]包括2个结点。
3)继续合并,加入第二个朋友关系(1, 3)。
(5)查找。查找某个结点属于哪个集 。这是一个递归 的过程,例如找结点1的集,递归步骤是:set[1] = 2、set[2] = 3、set[3] = 4、set[4] = 4,最后结点的值和它的集相等 ,就找到了根结点的集。
(6)统计。统计有几个集。只要检查有多少结点的集等于自己,就有几个集 。如果s[i] = i,这是一个根结点,是它所在的集的代表;统计根结点的数量,就是集的数量。上面的图示中,只有set[4] = 4、set[5] = 5,有2个集。
例子——
hl:x 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 #include <bits/stdc++.h> using namespace std;const int N = 8e5 +5 ;int s[N];void init_set () for (int i=1 ; i<=N; i++) s[i] = i; } int find_set (int x) return x==s[x]? x:find_set (s[x]); } void merge_set (int x, int y) x = find_set (x); y = find_set (y); if (x != y) s[x] = s[y]; } int main () init_set (); int n,m; cin>>n>>m; while (m--){ int op,x,y; cin>>op>>x>>y; if (op == 1 ) merge_set (x, y); if (op == 2 ){ if (find_set (x)==find_set (y)) cout << "YES" <<endl; else cout << "NO" <<endl; } } return 0 ; }
代码超时 !合并的时候,树变成了一个链表形状,出现了“退化”。下面用路径压缩来解决退化问题。
路径压缩
在上面的查询程序find_set()中,查询元素i所属的集,需要搜索路径找到根结点,返回的结果是根结点。这条搜索路径可能很长,导致超时。
如何优化?如果在返回 的时候,顺便把i所属的集改成根结点 ,那么下次再查的时候,就能在O(1)的时间内得到结果。由于find_set()是一个递归函数,在返回的时候,整个递归路径上的点,它们的集都改成了根结点。如下图所示,查询点1的集时,把路径上的2、3所属的集一起都改成了4,最后所有的结点的集都是4,下次再查询某个点所属的集,只需查一次。
1 2 3 4 5 6 int find_set (int x) if (x != s[x]) s[x] = find_set (s[x]); return s[x]; }
刚刚例题不超时代码
hl:"s[x] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 #include <bits/stdc++.h> using namespace std;const int N = 8e5 +5 ;int s[N];void init_set () for (int i=0 ; i<N; i++) s[i] = i; } int find_set (int x) if (x != s[x]) s[x] = find_set (s[x]); return s[x]; } void merge_set (int x, int y) x = find_set (x); y = find_set (y); if (x != y) s[x] = s[y]; } int main () init_set (); int n,m; cin>>n>>m; while (m--){ int op,x,y; cin>>op>>x>>y; if (op == 1 ) merge_set (x, y); if (op == 2 ){ if (find_set (x)==find_set (y)) cout << "YES" <<endl; else cout << "NO" <<endl; } } return 0 ; }
找共几类 找一共有几类
1 2 3 4 5 6 unordered_set<int > Sets; for (int i = 1 ; i <= PlantNum; i++) { Sets.insert (find_set (i)); } cout << Sets.size () << endl;
找每个集合有多少 通过setSum数组,在合并时双方都增加
hl:setSum 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 void init_set () for (int i = 1 ; i <= N; i++) { myset[i] = i; setSum[i] = 1 ; } return ; } void merge_set (int x, int y) x = find_set (x); y = find_set (y); if (x != y) { myset[x] = myset[y]; int numX = setSum[x]; int numY = setSum[y]; setSum[x] += numY; setSum[y] += numX; } return ; }
你总是忘记init
最小生成树和最大生成树 生成树(spanning tree) :一个连通无向图的生成子图,同时要求是树。也即在图的边集中选择n-1条,将所有顶点连通。
最小生成树 kruskal实现 核心思想:从小到大加入边,是个贪心算法。也接住了并查集的思路
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 #include <bits/stdc++.h> #define inf 0x7f7f7f7f using namespace std;typedef long long ll;const int N=2e5 +5 ;int n,m;ll ans; struct edge { int u,v,w; }e[N]; int f[5005 ],add=1 ;bool cmp (edge a,edge b) return a.w<b.w;}inline int find (int k) if (f[k]==k) return k; else return f[k]=find (f[k]); } inline void link (int a,int b) f[find (b)]=find (a); } int main () ios::sync_with_stdio (false ); cin.tie (0 );cout.tie (0 ); for (int i=0 ;i<5005 ;i++)f[i]=i; cin>>n>>m; for (int i=0 ;i<m;i++){ int a,b,c; cin>>a>>b>>c; e[i]=(edge){a,b,c}; } sort (e,e+m,cmp); for (int i=0 ;i<m&&add<=n;i++){ int u=e[i].u,v=e[i].v,w=e[i].w; if (find (u)!=find (v)){ link (u,v); ans+=w; add++; } } if (add!=n)cout<<"orz" ; else cout<<ans; return 0 ; }
最大生成树
方法1:将边权从大到小排序。
方法2:将所有边权取反(负数)
LCA 最近公共祖先 基本方法 找两个结点的最近公共祖先
在找a和b的LCA时,先让a和b中深度较大的那一个,向上回溯到与另一个同样深度的位置上。例如下面这个图:
假设要找F和E的LCA,先让F向上回溯 到他的父节点D 的位置,这样就与E处在同一深度 了。然后让他们同时向上回溯 (跳到他们的父节点上),直到两者相遇。相遇时所到达的那个点就是他们的LCA。这种方法很容易理解也很好实现,只需要对树进行一次深度搜索,在搜索过程中将每个点的父节点和他的深度保存下来即可进行上述的查询操作了,结合查询函数代码理解一下:1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 int fa[100 ],deep[100 ];int LCA (int a,int b) if (deep[a]<deep[b]) swap (a,b); while (deep[a]>deep[b]) b=deep[b]; while (a!=b) { a=deep[a]; b=deep[b]; } return a; }
而这种方法最大的问题就是运行太慢了,只能一步一步的往上跳,在很多场景下是不可取的。下面介绍倍增法,这种方法与上面的思路基本一样,但不是一步一步的向前跳
倍增法 关键理论:
将2的次幂排成一个序列,即1,2,4,8,16,32……在这个序列中取任意个不相等的数 ,相加可以得到所有正整数 。例如5=1+4;10=2+8;20=4+16,也就是每个正整数都可以拆分成多个2的幂次数 。拆分方法也很简单:例如20这个数,先找最接近但不大于20的一个2的幂次数,即16,然后20减去16等于4。再找最接近但不大于4的一个2的幂次数,即4。然后4-4=0,拆分结束,得到了16和4。
如果c是a和b的LCA,那么c的所有祖先同样也是a和b的公共祖先,但不是最近的。
倍增法中的ST 在ST算法中,我们维护了一个数组DP[i][j],表示的是以下标为i为起点的长度为2^j的序列的信息。然后用动态规划的思想求出整个数组。刚才在上面说我们求LCA时一次要跳2的幂次方层,这就与DP数组中下标 j 的定义不谋而合了。
所以我们定义倍增法中的DP[i][j]为:结点 i 的向上 2^j 层的祖先。
DP[4][1]=1;结点4的向上2^1=2层的祖先是结点1。
【递推式】DP[i][j] = DP[ DP[i][j-1] ] [j-1]:DP[i][j-1]是结点i往上跳2^(j-1)层的祖先,那我们就在跳到这个结点的基础上,再向上跳2^(j-1)层 ,这样就相当于从结点i,先跳2^(j-1)层,再跳2^(j-1)层,最后还是到达了2^j层 。
1 2 3 4 5 6 7 8 9 10 11 12 int fa[100 ],DP[100 ][20 ];void init () for (int i=1 ;i<=n;i++) dp[i][0 ]=fa[i]; for (int j=1 ;(1 <<j)<=n;j++) for (int i=1 ;i<=n;i++) DP[i][j]=DP[DP[i][j-1 ]][j-1 ]; }
查询函数
假设a和b的深度相差5,我们需要让b向上跳,步步逼近a所在的深度,直到与a同深度。如何选取这个步长呢?两个原则:选取的步长肯定不能大于二者的深度差 ,否则b的深度就小于a的了;最接近深度差但又不大于深度差的2的幂次数 。这使我们每一步都不会超出a,而且步步逼近a。
第二次回溯与第一次不同的是:第一次回溯,已经知道了要跳多少层 ,所以就可以用正整数拆分理论选择步长。而这次回溯是要找LCA ,即找一个层数使a和b跳上去之后正好相遇,也就是说我们只能试探着往上跳,步步逼近。跳到了某一层后a和b相遇了,则说明相遇处的结点就是a和b的公共祖先 ,但不一定是最近 的。这个点就告诉我们:LCA可能还在这个点的下方。那我们就不往这个点上跳 ,因为这个点有可能不是我们要找的LCA。则说明a和b的LCA在这层之上 ,那我们完全可以跳到这一层上,这会使我们步步逼近最终的LCA 。根据正整数拆分理论,我们最后也一定能找到LCA。
第二次回溯。换个角度讲,假设我们事先知道LCA与a、b差10层,那么我们如果一步跳了10层以上的话,肯定会跳到LCA的祖先上 ,那我们就减少步长。如果一步跳8层的话,a和b肯定没有相遇 ,这时我们就可以跳上来。然后LCA与a、b就差两层了。虽然再跳两层就到了,但是程序只知道这是a和b的公共祖先,但不知道这是不是最近公共祖先,而我们只是开了上帝视角知道了而已,所以程度就会放弃2这个步长,还会将步长减小为1并跳上去。当步长减小为1时,这个试探的过程就可以结束了,因为LCA肯定就是此时a和b的父节点。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 int LCA (int a,int b) if (dep[a]<dep[b]) swap (a,b); for (int i=19 ;i>=0 ;i--) { if (dep[a]-(1 <<i)>=dep[b]) a=dp[a][i]; } if (a==b) return a; for (int i=19 ;i>=0 ;i--) { if (dp[a][i]!=dp[b][i]) { a=dp[a][i]; b=dp[b][i]; } } return dp[a][0 ]; }
链式前向星(加快图的搜索) 存储一个图通常有两种方式:邻接矩阵和邻接表。如果一个图中的边非常少,那么邻接矩阵就比较稀疏 ,浪费空间,如果点非常多,则矩阵的内存有可能会爆掉 。用向量实现的邻接表在点非常多的时候同样比较慢,在一些题目中会超时。链式前向星是在邻接表基础上的一种优化,其优秀的时空复杂度可以帮助我们在一些边和点都比较多情况下加快对图的遍历。例如DFS、BFS等。我们可以结合DFS的过程来理解链式前向星。
DFS算法的实现过程可以这样理解:
以当前点作为起点,在所有与该起点连接着的边中随便找一条 ,然后跳到这条边的终点上 。
再将当前跳到的点当做起点,重复1。
若跳到某一点后,没有以这个点为起点的边了,就原路返回到之前的起点上 ,找一条与这条不同的边,再跳到它的终点上。
【数据结构】1 2 3 4 5 struct node { int to; int next; }edge[maxn];
链式前向星以边为单位 进行储存。其中,成员to表示这条边的终点 ,而next就比较重要了,表示跟本条边的起点相同的前一条边 ,在edge数组中的下标 ,如果这条边的起点是第一次出现的,则置为0。也就是说,链式前向星的next属性,像链表一样,将图中起点相同的边连在了一起。例如下面这个图:
那么我们得到的edge数组为:
下标
1
2
3
4
5
6
7
起点
1
2
3
4
1
1
4
to
2
3
4
5
3
5
1
next
0
0
0
0
1
5
4
以下标为5来讲,建立<1,3>边,而<1,2>边具有相同的起点,其下标为1,所以<1,3>的next为1.
当我们想要得到一条边的终点时,就调用edge[i].to,当我们想得到这个起点连接的其他边时,就可以调用edge[i].next。那么现在的问题就是如何快速求next属性。
解决方法就是再定义一个数组head,head[i]表示最近一次输入的以i为起点的边在edge数组中的下标 。
【建立图】1 2 3 4 5 6 7 8 9 10 11 12 13 14 struct node { int to; int next; }edge[maxn]; int head[maxn];int cnt=1 ;void add (int from,int t) edge[cnt].to=t; edge[cnt].next=head[from]; head[from]=cnt; cnt++; }
【遍历图】
核心for(int i=head[x];i!=0;i=edge[i].next)
在对某一点所连接的所有边的遍历过程中,调用edge[i].next,就像链表一样,将所有起点相同的边都串在了一起。而且,最先输入的边会最晚遍历到,这是由next的属性所造成的 。
hl:"int i 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 #include <iostream> using namespace std;const int maxn=1000 ;struct node { int to; int next; }edge[maxn]; int head[maxn];int cnt=1 ;void add (int from,int t) edge[cnt].to=t; edge[cnt].next=head[from]; head[from]=cnt++; } bool s[maxn];void dfs (int x) s[x]=true ; printf ("%d " ,x); for (int i=head[x];i!=0 ;i=edge[i].next) { if (!s[edge[i].to]) dfs (edge[i].to); } } int main () int u,v,w; int n; cin>>n; while (n--) { cin>>u>>v; add (u,v); } dfs (1 ); return 0 ; }
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 #include <iostream> #include <queue> #include <cstdio> using namespace std;const int maxn=500005 ;struct node { int to; int next; }e[2 *maxn]; int head[maxn];int cnt;void add (int a,int b) e[++cnt].to=b; e[cnt].next=head[a]; head[a]=cnt; } bool vis[maxn];int main () int n,u,v; cin>>n; while (n--) { cin>>u>>v; add (u,v); } queue<int > q; q.push (1 ); while (!q.empty ()) { int temp=q.front (); q.pop (); vis[temp]=true ; printf ("%d " ,temp); for (int i=head[temp];i;i=e[i].next) { if (!vis[e[i].to]) q.push (e[i].to); } } return 0 ; }
最终代码 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 #include <iostream> #include <vector> #include <cstdio> using namespace std;const int maxn=500005 ;int root,n,m,a,b,c;struct node { int to; int next; }e[2 *maxn]; int head[maxn];int cnt;void add (int a,int b) e[++cnt].to=b; e[cnt].next=head[a]; head[a]=cnt; } int fa[maxn][20 ],dep[maxn];void dfs (int root,int pre) dep[root]=dep[pre]+1 ; fa[root][0 ]=pre; for (int i=1 ;(1 <<i)<=dep[root];i++) fa[root][i]=fa[fa[root][i-1 ]][i-1 ]; for (int i=head[root];i;i=e[i].next) { if (e[i].to!=pre) dfs (e[i].to,root); } } int LCA (int a,int b) if (dep[a]<dep[b]) swap (a,b); for (int i=19 ;i>=0 ;i--) { if (dep[a]-(1 <<i)>=dep[b]) a=fa[a][i]; } if (a==b) return a; for (int i=19 ;i>=0 ;i--) { if (fa[a][i]!=fa[b][i]) { a=fa[a][i]; b=fa[b][i]; } } return fa[a][0 ]; } int main () cin>>n>>m>>root; for (int i=1 ;i<n;i++) { scanf ("%d%d" ,&a,&b); add (a,b); add (b,a); } dfs (root,0 ); while (m--) { scanf ("%d%d" ,&a,&b); printf ("%d\n" ,LCA (a,b)); } return 0 ; }
图 最短路径 单源最短路径 即起点固定已经知道了。(终点可以查询)
无边权 即每条边的权相同
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 void bfs (vector<unordered_set<int >> &myEgde, int start, int end) int d[500 ] = {INT_MAX}; int path[500 ] = {-1 }; bool visit[500 ] = {false }; d[start] = 0 ; visit[start] = true ; deque<int > myDeque; myDeque.push_back (start); while (!myDeque.empty ()) { int now = myDeque.front (); myDeque.pop_front (); for (const auto &next : myEgde[now]) { if (!visit[next]) { d[next] = d[now] + 1 ; path[next] = now; visit[next] = true ; myDeque.push_back (now); } } } cout << d[end] << endl; return ; }
迪杰斯特拉(有边权) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 #include <bits/stdc++.h> using namespace std;#define INF 0x3f3f3f3f3f3f3f3f using ll = long long ;struct Edge { int to; ll weight; }; int main () ios::sync_with_stdio (false ); cin.tie (0 ); cout.tie (0 ); int N, M; cin >> N >> M; vector<vector<Edge>> G (N + 1 ); int i, j, k; for (i = 0 ; i < M; i++) { int u, v, w; cin >> u >> v >> w; G[u].push_back ({ v, w }); } vector<ll> dist (N + 1 , INF) ; dist[1 ] = 0 ; priority_queue<pair<ll, int >, vector<pair<ll, int >>, greater<pair<ll, int >>> Q; Q.push ({ 0 , 1 }); while (!Q.empty ()) { auto [d, u] = Q.top (); Q.pop (); if (d > dist[u]) continue ; for (const auto &[v, w] : G[u]) { if (dist[u] + w < dist[v]) { dist[v] = dist[u] + w; Q.push ({ dist[v], v }); } } } for (j = 1 ; j <= N; j++) { if (dist[j] == INF) cout << "-1" << " " ; else cout << dist[j] << " " ; } return 0 ; }
SPFA 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 int spfa () memset (dist, 0x3f , sizeof dist); dist[1 ] = 0 ; queue<int > q; q.push (1 ); st[1 ] = true ; while (heap.size ()) { int t = q.front (); q.pop (); st[t] = false ; for (int i = h[t]; i != -1 ; i = ne[i]) { int j = e[i]; if (dist[j] > dist[t] + w[i]) { dist[j] = dist[t] + w[i]; if (!st[j]) { q.push (j); st[j] = true ; } } } } if (dist[n] == ox3f3f3f) return -1 ; return dist[n];
多源最短路 即起点和终点的目标每次不一样,对同一个图有多次查询。使用Floyd算法
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 #include <bits/stdc++.h> using namespace std;long long INF = 0x3f3f3f3f3f3f3f3f ; int n, m, t;long long dp[500 ][500 ]; void input () int x, y; long long z; scanf ("%d %d %d" , &n, &m, &t); for (int i = 0 ; i < m; i++) { scanf ("%d %d %lld" , &x, &y, &z); dp[x][y] = dp[y][x] = min (dp[x][y], z); } } void Floyd () for (int k = 1 ; k <= n; k++) { for (int i = 1 ; i <= n; i++) for (int j = 1 ; j <= n; j++) dp[i][j] = min (dp[i][j], dp[i][k] + dp[k][j]); } } void ouput () int v, u; while (t--) { scanf ("%d %d" , &v, &u); if (dp[v][u] == INF) printf ("-1\n" ); else if (v == u) printf ("0\n" ); else printf ("%lld\n" , dp[v][u]); } } int main () for (int i = 0 ; i <= 500 ; i++) { for (int k = 0 ; k <= 500 ; k++) dp[i][k] = INF; } input (); Floyd (); ouput (); return 0 ; }
联通分量与桥、环 Tarjan算法 请参考文章 ;力扣文章
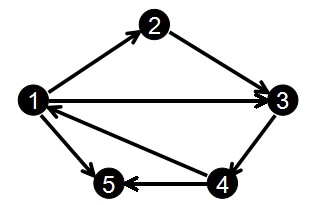
如果某一个子图的任意两点都是连通(注意:有向图需要双向联通,或者是环) 的则该子图是一个强连通分量。
在一个顶点数为n的图中,Tarjan算法需要维护一个顶点栈和几个数组。
stack S:表示顶点栈。dfn[i]:表示第i个顶点的深度搜索次序。(可以理解为遍历到这个点的时间)low[i]:表示顶点i回溯时所能回溯到的最小dfn。(最早遍历时间)
从当前节点 x 作为搜索树的根节点出发,能够访问到的所有节点中,时间戳最小的值 —— low[x]
什么是“能够访问到的所有节点”?,其需要满足下面的条件之一即可:
以 x 为根的搜索树的所有节点
通过一条非搜索树 上的边,能够到达搜索树的所有节点
什么是搜索树:在无向图中,我们以某一个节点 x 出发进行深度优先搜索,每一个节点只访问一次,所有被访问过的节点与边构成一棵树,我们可以称之为“无向连通图的搜索树”。
在上面的计算过程中,我们可以认为以序号 2 为根的搜索树的节点有 {2,3,4,5}。上面所说的“通过一条非搜索树上的边”可以理解成动画中的(1,5)这条边,“能够到达搜索树的所有节点”即为节点 1。
visit[i]:表示顶点i是否在栈中。color[i]:表示顶点i在哪一个强连通分量,相同的强连通分量染色相同。
桥的判定 在一张无向图中,判断边 e (其对应的两个节点分别为 u 与 v)是否为桥,需要其满足如下条件即可:dfn[u] < low[v]
它代表的是节点 u 被访问的时间,要优先于(小于)以下这些节点被访问的时间 —— low[v]
以节点 v 为根的搜索树中的所有节点
通过一条非搜索树上的边,能够到达搜索树的所有节点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 class Solution {public : vector<vector<int >> edgs; vector<int > dfn; vector<int > low; vector<bool > visit; vector<vector<int >> ret; int times; void tarjan (int node, int parent) times++; dfn[node] = times; low[node] = times; visit[node] = true ; for (auto e : edgs[node]){ if (e == parent) continue ; if (!visit[e]){ tarjan (e, node); low[node] = min (low[e], low[node]); if (low[e] > dfn[node]){ ret.push_back ({node, e}); } }else { low[node] = min (low[node], dfn[e]); } } } vector<vector<int >> criticalConnections (int n, vector<vector<int >>& connections) { dfn = vector <int >(n,0 ); low = vector <int >(n,0 ); visit = vector <bool >(n,false ); edgs = vector<vector<int >>(n); times = 0 ; for (auto & conn : connections){ edgs[conn[0 ]].push_back (conn[1 ]); edgs[conn[1 ]].push_back (conn[0 ]); } tarjan (0 ,0 ); return ret; } };
视频 )
上图黄色的为回溯的部分
理解:为什么需要parent?
理解:为什么low[node] = min(low[e], low[node]);?low[node] = min(low[node], dfn[e]);;然后low[5]就被置为dfn[6]=1了,继续回溯,(走黄色部分)到7,low[7] = min(low[7], low[5]);然后就统一了。
在回溯的时候,就已经更新 了,所以可以马上判断是否是桥 !
经过实战,在判断桥时,统一写为min(low[node], low[e]);也没有问题。
割点 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 for (int i=1 ;i<=n;i++) if (DFN[i]==0 ) tarjan (i,i); void tarjan (int u, int fa) dfn[u] = low[u] = ++id; int child = 0 ; for (int i = head[u]; i; i = e[i].nxt) { int to = e[i].to; if (!dfn[to]) { tarjan (to, fa); low[u] = min (low[u], low[to]); if (low[to]>=DFN[u]&&u!=fa) cut[u]=1 ; if (u==fa) child++; } else { low[u] = min (low[u], dfn[to]); } if (child>=2 &&u==fa) cut[u]=1 ; } } for (int i = 1 ; i <= n; i++) { if (cut[i]) { ans++; } }
为什么这里判断割点,条件稍微有点不一样?
首先,low[to] > dfn[u],肯定算割点(因为都是桥了)(u!=fa)
low[to]=dfn[u]:满足这个情况的有两类点
即最开始的根结点。比如下图,如果从3开始算的话,3本身就是割点!(注意:图示从1开始算)
或者一个桥,的另一边,如上一节桥的6号结点(u!=fa)
联通分量的判定 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 void Tarjan (int u) cnt++; dfn[u]=low[u]=cnt; S.push (u); visit[u]=1 ; for (int i=head[u];i;i=last[i]){ int v=to[i]; if (!dfn[v]){ Tarjan (v); low[u]=min (low[u],low[v]); }else if (visit[i]){ low[u]=min (low[u],dfn[v]); } } if (dfn[u]==low[u]){ color[u]=++sum; visit[u]=0 ; while (S.top ()!=u){ color[S.top ()]=color[u]; visit[S.top ()]=0 ; S.pop (); } } }
拓扑排序 拓扑排序思路:入度为0的点入栈 ,如果-1后为0邻接表相应点入栈 。len(res) ==n,则代表所有点都有遍历到
基于DFS的拓扑算法 对于图中的任意一个节点,它在搜索的过程中有三种状态,即:
「未搜索」:我们还没有搜索到这个节点;
「搜索中」:我们搜索过这个节点,但还没有回溯到该节点,即该节点还没有入栈,还有相邻的节点没有搜索完成);
「已完成」:我们搜索过并且回溯过这个节点,即该节点已经入栈,并且所有该节点的相邻节点都出现在栈的更底部的位置,满足拓扑排序的要求。
通过上述的三种状态,我们就可以给出使用深度优先搜索得到拓扑排序的算法流程,在每一轮的搜索搜索开始时,我们任取一个「未搜索」的节点开始进行深度优先搜索。
我们将当前搜索的节点 uu 标记为「搜索中」,遍历该节点的每一个相邻节点 vv:
如果 v为「未搜索」,那么我们开始搜索 v,待搜索完成回溯到 u;
如果 v 为「搜索中」,那么我们就找到了图中的一个环,因此是不存在拓扑排序的;
如果 v 为「已完成」,那么说明 v 已经在栈中了,而 u 还不在栈中,因此 u 无论何时入栈都不会影响到 (u, v)(u,v) 之前的拓扑关系,以及不用进行任何操作。
当 u 的所有相邻节点都为「已完成」时,我们将 u 放入栈中,并将其标记为「已完成」。
在整个深度优先搜索的过程结束后,如果我们没有找到图中的环,那么栈中存储这所有的 n 个节点,从栈顶到栈底的顺序即为一种拓扑排序。
基于BFS 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 class Solution {public : vector<int > findOrder (int numCourses, vector<vector<int >>& prerequisites) { unordered_map<int ,vector<int >> edges; vector<int > in (numCourses,0 ) ; for (vector<int >& e:prerequisites){ int a=e[0 ],b=e[1 ]; edges[b].push_back (a); in[a]++; } queue<int > q; vector<int > ret; for (int i=0 ;i<numCourses;++i) if (in[i]==0 ){ q.push (i); ret.push_back (i); } while (!q.empty ()){ int t=q.front (); q.pop (); for (int e:edges[t]){ in[e]--; if (in[e]==0 ){ q.push (e); ret.push_back (e); } } } for (int i:in) if (i) return {}; return ret; } };






/lowbitx.png)















/KMP匹配.png)
/KMP伪代码1.png)
/KMP伪代码2.png)
/并查集.png)
/并查集2.png)
/并查集3.png)
/并查集之蓝桥幼儿园.png)
/并查集之路径压缩.png)


/tarjan算法.png)

/tarjan割点.png)
/拓扑排序排序不唯一,比如这里有两个选择.png)








