CNN入门

CNN就是一种特殊的前馈神经网络。

这两者的主要区别在于，CNN在前馈神经网络的基础上加入了卷积层和池化层（下边会讲到），以便更好地处理图像等具有空间结构的数据。

为什么我们需要CNN？

在用全连接前馈网络来处理图像时，会存在以下几个问题：

1. 参数太多：如果输入图像大小为$100100$（即图像高度为100，宽度为100，单颜色通道），那么第一个隐藏层的每个神经元到输入层都有$100100=10000$个互相独立的连接
2. 不利于表达空间结构
3. 难以反映平移不变性

卷积之前

何谓卷积

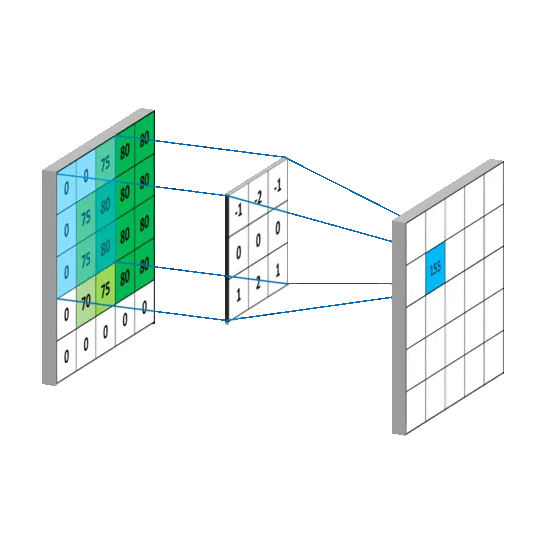
当一组数像滑窗一样滑过另外一组数时，将对应的数据相乘并求和得到一组新的数，这个过程必然和卷积有着莫大的关系。

中间的矩阵就是所谓的卷积核。卷积核并不是手动设计出来的，而是通过数据驱动的方式学习得到的。

步长

步长描述的是在进行卷积操作时，卷积核在输入数据上移动的距离

在两维图像中，步长通常是一个二元组，分别代表卷积核在垂直方向（高度）和水平方向（宽度）移动的单元格数。
例如，步长为1意味着卷积核在每次移动时，都只移动一个单元格，这就意味着卷积核会遍历输入数据的每一个位置；同理，如果步长为2，那么卷积核每次会移动两个单元格。

零填充（zero-padding）

如图，卷积核从左上角开始扫描时，每条边只能滑动三次。如果定义输入层的边长是M，卷积核的边长是K，那么卷积后输出的边长是M-K+1。

那么这样一直算到后边，尺寸岂不是要变成1了？对此，解决办法就是在输入数据进行卷积运算前，在四周补充一圈（或多圈）数字，通常补充的是0，所以就叫“零填充”

此时卷积输出的矩阵边长为：$L=(M-K+2P)/S+1$(填充的圈数P，以及步长的长度S)

池化层

池化层的主要作用是对非线性激活后的结果进行降采样，以减少参数的数量，避免过拟合，并提高模型的处理速度。

• 最大池化（Max Pooling）:选取窗口最大的值
• 平均池化：选取窗口平均值

参数更新与迭代

参考资料：
[1] https://zhuanlan.zhihu.com/p/635438713