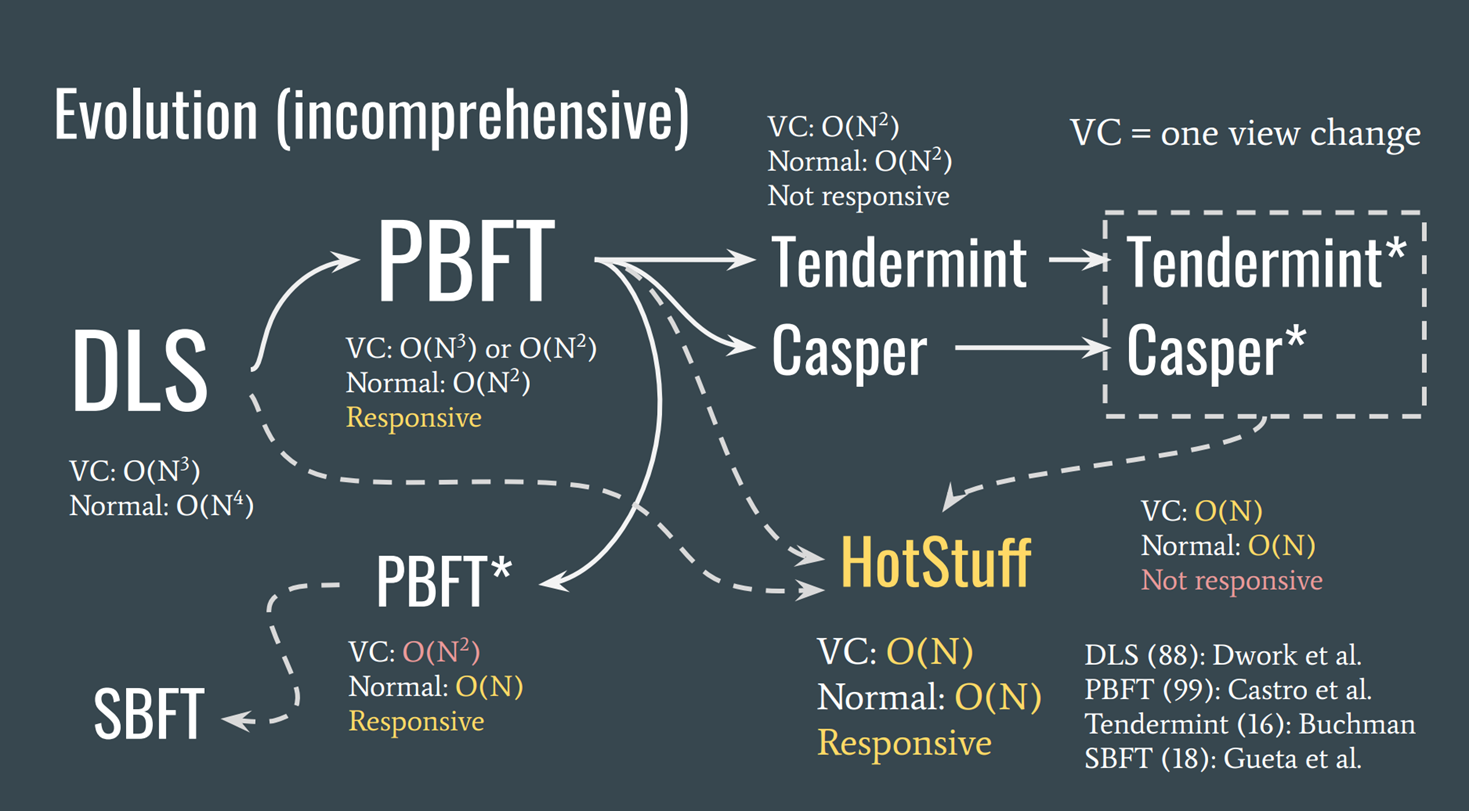
区块链双链

现存挑战
- 性能——我要存储很多区块来记账
- 隐私性——任何结点都可以访问区块链隐私性难以论证
解决方案
- 性能——轻量化区块头（部分结点只需记录区块头即可）
- 隐私性——双链保护

双链顾名思义是两条链

1. 私有链+联盟链

可以参考车载网论文

私有链仅可信结点访问，保存真实名字——虚假名字——公钥——私钥——过期时间
联盟链基本全局可以访问，保存虚假名字——公钥

私有链可以保证可追溯性
联盟链可以保证去标识化

前沿密码学

代理重加密

由于大部分的云服务供应商并不能完全值得信任，云服务供应商可能会在未经用户允许的情况下，擅自泄露用户的隐私数据或重要文件。

解决这个问题最直接的方法是数据加密，对于涉及用户隐私或含有敏感信息的数据文件，将数据加密后上传是一种普遍的保证数据机密性的方法，这样数据上传者只需保管好解密密钥即可。

但是云计算服务中存在大量的需要共享数据的应用需求，对于这种简单的数据加密上传方式，由于加密文件只能被用户自行解密，这样的数据加密文件并不能通过云服务器来分享给他人，为此这便需要一种密码方案，使得能对存储在云服务器上的密文进行安全有效的转换。

PRE 技术可以将用户 A 用自己公钥加密上传的密文转换成另一种形式的密文，使得用户 B 可以用自己私钥对转换后的密文进行解密，并且在整个转换过程中不会泄露任何对应的明文信息

在代理重加密中，基于授权人(delegator)公钥加密的密文可以被转换为另一种密文，且保持对应明文不变，被转换后的密文可以由被授权人(delegate)的私钥进行解密。该密文转换过程由一个半可信的代理者(proxy)执行，在执行该过程前，代理者需要持有一个由授权人到被授权人的转换密钥，该转换密钥一般由授权人事先生成并交给代理者。同时在密文转换的整个过程中，代理者无法获取关于该密文对应明文的任何信息。

具体过程

代理重加密实现过程

对比

Alice通过半信任的proxy，发送消息Bob。她使用公钥pk1加密了自己的消息，并上传到云服务器。这个消息是安全的，因为只有她自己拥有私钥pk1。几周后，Bob来了，他需要查看这个消息。

这个时候，Alice有两个选择。

1 Alice解密消息，拿到Bob的公钥pk2，使用pk2加密消息，并发送给Bob。这个方法的缺点是，如果有多个Bob的话，这种方法会很麻烦。（另一个缺点是，Alice需要保存所有历史消息，而下一种方法不必保存。）

2 Alice拿到Bob的公钥pk2，生成一个重加密密钥delkey，并上传到Proxy，Proxy使用这个delkey对加密消息，再进行一次加密，生成newCipherText。Bob下载这个重加密消息，并使用自己的私钥sk2解密。

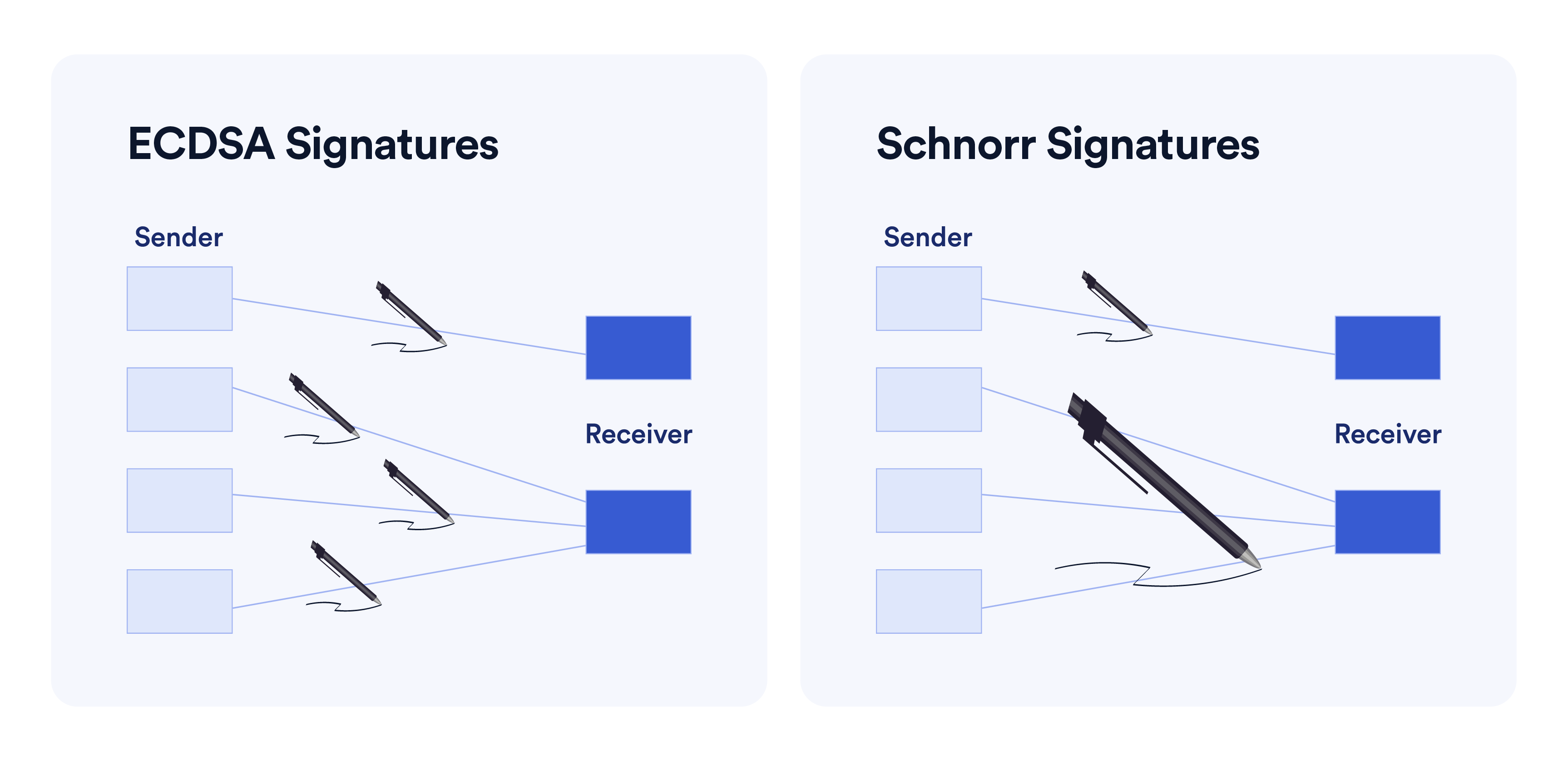
Schnorr

签名聚合使得多个签名者的签名可以合并为一个单一的签名

【看不懂版】

1.1 密钥生成

Schnorr签名算法使用椭圆曲线密码学作为基础，首先需要生成公私钥对。具体步骤如下：

选择一个椭圆曲线E。
随机选择一个私钥𝑑，其中0 < 𝑑 < ord(E)，ord(E)为椭圆曲线的阶（阶是指：_椭圆曲线上的点的数目_）。
计算公钥𝑄 = 𝑑 × G，其中G为椭圆曲线的基点。

其中，𝑑为私钥，𝑄为公钥。

1.2 签名生成

假设要对消息𝑚进行签名，具体步骤如下：

随机选择一个整数𝑘，其中0 < 𝑘 < ord(E)。
计算椭圆曲线上的点𝑅 = 𝑘 × G。
计算哈希值ℎ = Hash(𝑚)。
计算𝑠 = (𝑘 - 𝑑 × ℎ) mod ord(E)。

其中，𝑅为签名中的随机因子，𝑠为签名中的部分签名值。

最终的签名为(𝑅, 𝑠)。

1.3 签名验证

我看不懂
在接收到签名(𝑅, 𝑠)和消息𝑚后，验证签名的有效性。具体步骤如下：

计算哈希值ℎ = Hash(𝑚)。
计算验证因子𝑤 = ℎ^(-1) mod ord(E)。——哈希值 ℎh 在椭圆曲线阶 𝑜𝑟𝑑(𝐸)ord(E) 下的乘法逆元——乘法逆元是存在一个元素与给定元素相乘后得到单位元，常用“费马小定理”求解

如果p是质数，那么a的乘法逆元是a^(p-2)（mod p），前提是a与p互质

计算椭圆曲线上的点𝑢₁ = 𝑠 × 𝑤 × G + (-𝑤 × ℎ) × 𝑄。
计算哈希值ℎ’ = Hash(𝑚)。
如果𝑅 = 𝑢₁ + 𝑤 × ℎ’ × G，则验证通过；否则验证失败。

【讲的更清楚版】

schnorr签名的基础定义

密钥 k 和 R 称为 “一次性的” 是有原因的：如果你使用相同的密钥签署两条不同的消息，你将泄露整个私钥

Schnorr签名

签名可以被聚合

可编辑区块链

变色龙哈希函数

任何人可以通过给定的公钥$pk$进行变色龙哈希后，拥有$sk$的用户可以广义地找到哈希碰撞，即使得 $Ch_Hash(m’)=Ch_Hash(m)$

4个主要的算法：
- 密钥生成算法$Ch_gen(1^{\lamda})=(sk,pk)$ 给定一个安全常数λ ，输出变色龙哈希的公钥pk和私钥sk（陷门）
- 哈希生成：输入公钥pk、随机数r和任意消息m，生成哈希值h和随机数p
- 哈希验证算法：输入公钥pk、任意消息m和哈希值h、随机数p，若( h , p )是正确的哈希值，则输出1，否则输出0；
- 哈希碰撞算法：

变色龙哈希的安全需求

1）抗碰撞性：在没有陷门$sk$的情况下，输入消息$m_1$、随机数$r_1$和消息$m_2$，满足$Hash(m_1,r_1)=Hash(m_2,r_2)$ 的整数$r_2$是几乎不可能的。
2）陷门碰撞：在输入陷门sk后，对于任意的$m_1,r_1$，给定消息$m_2$，可以计算出$r_2$，满足$Hash(m_1,r_1)=Hash(m_2,r_2)$。
3）语义安全：对于任意消息$m1,m2$，他们的$Hash(m_1,r_1)$和$Hash(m_2,r_2)$的概率分布在计算上是不可区分的。
.png)