引入

序言

KNN 在我们日常生活中也有类似的思想应用，比如，我们判断一个人的人品，往往只需要观察他最密切的几个人的人品好坏就能得到结果了。

KNN 方法既可以做分类，也可以做回归

分类问题的数学抽象

分类问题数学抽象

我们的训练数据会被映射成 $\ n$ 维空间的样本点（这里的 $\ n$ 就是特征维度），我们需要做的事情是对 $\ n$ 维样本空间的点进行类别区分，某些点会归属到某个类别。

算法核心思想

K近邻核心思想

在 KNN 分类中，输出是一个分类族群。一个对象的分类是由其邻居的「多数表决」确定的，$\ K$ 个最近邻居（ $\ K$ 为正整数，通常较小）中最常见的分类决定了赋予该对象的类别。

  • 若 K=1，则该对象的类别直接由最近的一个节点赋予。

    在 KNN 回归中，输出是该对象的属性值。该值是其 $\ K$ 个最近邻居的值的平均值。

豆子分类例子

三个豆的种类未知，如何判定他们的种类

思路是——未知的豆离哪种豆最近，就认为未知豆和该豆是同一种类。

最近邻算法的定义：为了判定未知样本的类别，以全部训练样本作为代表点计算未知样本与所有训练样本的距离，并以最近邻者的类别作为决策未知样本类别的唯一依据。

根据 $\ K$ 近邻算法，离绿点最近的三个点中有两个是红点，一个是蓝点，红点的样本数量多于蓝点的样本数量，因此未知的类别被判定为红点。

算法步骤

算法步骤

工作原理

  • 存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每个数据与所属分类的对应关系。

  • 输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签

算法示例

举例：以电影分类作为例子，电影题材可分为爱情片，动作片等。那么爱情片有哪些特征？动作片有哪些特征呢？也就是说给定一部电影，怎么进行分类？

这里假定将电影分为爱情片和动作片两类，如果一部电影中接吻镜头很多，打斗镜头较少，显然是属于爱情片，反之为动作片。

KNN算法及其应用; K近邻算法; 算法示例-电影分类;

有人曾根据电影中打斗动作和接吻动作数量进行评估，数据如图。给定一部电影数据 $\ (18,90)$ 打斗镜头 $\ 18$ 个，接吻镜头 $\ 90$ 个，如何知道它是什么类型的呢？

现在我们按照距离的递增顺序排序，可以找到 $\ K$ 个距离最近的电影。

KNN算法及其应用; K近邻算法; 算法示例-电影分类;

假如 $\ K=3$，那么来看排序的前 $\ 3$ 个电影的类别，都是爱情片，根据 KNN 的投票机制，我们判定这部电影属于爱情片。（这里的 $\ K$ 是超参数，可以调整，如果取 $\ K=4$，那可能投票的4部电影分别是 爱情片、爱情片、爱情片、动作片，但本例中判定结果依旧为爱情片）

核心要素

距离度量

KNN算法及其应用; K近邻算法; 核心要素-距离度量准则;

$\ Lp$ 距离（又称闵可夫斯基距离，Minkowski Distance）不是一种距离，而是一组距离的定义。

  • 参数 $\ p=1$ 时为曼哈顿距离（又称L1距离或程式区块距离），表示两个点在标准坐标系上的绝对轴距之和。
  • 参数 $\ p=2$ 时为欧氏距离（又称L2距离或欧几里得度量），是直线距离常见的两点之间或多点之间的距离表示法。
  • 参数 $\ p\rightarrow \infty$ 时，就是切比雪夫距离（各坐标数值差的最大值）

K的取值

在实际的应用中，一般采用一个比较小的 $\ K$ 值。并采用交叉验证的方法，选取一个最优的 $\ K$ 值。

缺点与改进

本质上是对于特征空间的划分。

  • 精度高、对异常值不敏感、无数据输入假定。
  • 计算复杂度高、空间复杂度高。
  • 适用于数值型

案例——房价的确定

问题背景

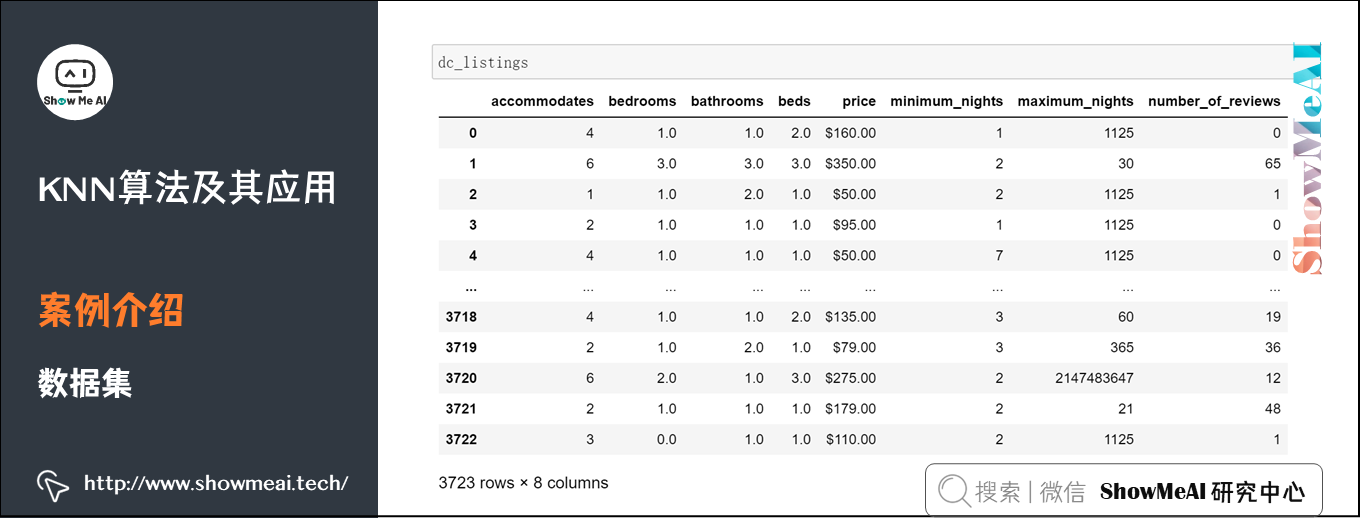
假如一套房子打算出租，但不知道市场价格，可以根据房子的规格（面积、房间数量、厕所数量、容纳人数等），在已有数据集中查找相似（K近邻）规格的房子价格，看别人的相同或相似户型租了多少钱

房屋出租价格预测数据集：https://pan.baidu.com/s/1UYkeEfLhESHFNTf9ogcg5A 提取码：show

分类过程

思路：将预计出租房子数据与数据集中每条记录比较计算欧式距离，取出距离最小的5条记录，将其价格取平均值，可以将其看做预计出租房子的市场平均价格。

1
2
3
4
5
6
import pandas as pd
import numpy as np
from scipy.spatial import distance#用于计算欧式距离
from sklearn.preprocessing import StandardScaler#用于对数据进行标准化操作
from sklearn.neighbors import KNeighborsRegressor#KNN算法
from sklearn.metrics import mean_squared_error#用于计算均方根误差
1
2
3
4
5
6
#导入数据并提取目标字段
path = r'rent_price.csv'
file = open(path, encoding = 'gb18030', errors = 'ignore')
dc_listings = pd.read_csv(file)
features = ['accommodates','bedrooms','bathrooms','beds','price','minimum_nights','maximum_nights','number_of_reviews']
dc_listings = dc_listings[features]

初步数据清洗

注意 ①：数据集中非数值类型的字段需要转换，替换掉美元$符号和千分位逗号。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#数据初步清洗
our_acc_value = 3  # 设置我们的accommodates值为3

# 计算每个列表项的距离值（以我们的acc_value为基准）
dc_listings['distance'] = np.abs(dc_listings.accommodates - our_acc_value)

# 随机打乱列表项的顺序
dc_listings = dc_listings.sample(frac=1, random_state=0)

# 按照距离值进行排序
dc_listings = dc_listings.sort_values('distance')

# 将price列中的美元符号和逗号去除，并转换为浮点数类型
dc_listings['price'] = dc_listings.price.str.replace("\$|,", "").astype(float)

# 删除包含NaN值的行
dc_listings = dc_listings.dropna()

注意 ②：理想情况下，数据集中每个字段取值范围都相同，但实际上这是几乎不可能的，如果计算时直接用原数数据计算，则会造成较大训练误差，所以需要对各列数据进行标准化或归一化操作，尽量减少不必要的训练误差。

1
2
3
4
5
6
7
8
9
10
#数据标准化
# 导入所需库
from sklearn.preprocessing import StandardScaler

# 使用StandardScaler对指定的features进行标准化处理
dc_listings[features] = StandardScaler().fit_transform(dc_listings[features])

# 将标准化后的dc_listings赋值给normalized_listings
normalized_listings = dc_listings

注意 ③：最好不要将所有数据全部拿来测试，需要分出训练集和测试集具体划分比例按数据集确定。

1
2
3
#取得训练集和测试集
norm_train_df = normalized_listings[:2792]
norm_test_df = normalized_listings[2792:]

计算并预测

利用sklearn

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# 选择第一项和第五项的指定特征列（accommodates和bathrooms）
first_listings = normalized_listings.iloc[0][['accommodates', 'bathrooms']]
fifth_listings = normalized_listings.iloc[20][['accommodates', 'bathrooms']]

# 使用多变量KNN模型预测价格
def predict_price_multivariate(new_listing_value, feature_columns):
    temp_df = norm_train_df
    # 计算temp_df中每个样本与新样本的距离（使用distance.cdist方法）
    temp_df['distance'] = distance.cdist(temp_df[feature_columns], [new_listing_value[feature_columns]])
    # 根据距离进行排序
    temp_df = temp_df.sort_values('distance')
    # 取距离最近的5个样本的价格并计算平均值作为预测价格
    knn_5 = temp_df.price.iloc[:5]
    predicted_price = knn_5.mean()
    return predicted_price

cols = ['accommodates', 'bathrooms']
# 对测试集中的每个样本应用多变量KNN模型，并将预测结果存储在新列predicted_price中
norm_test_df['predicted_price'] = norm_test_df[cols].apply(predict_price_multivariate, feature_columns=cols, axis=1)
# 计算预测值与实际值之间的平方误差的均值（均方误差）
mse = norm_test_df['squared_error'].mean()
# 计算均方误差的平方根（均方根误差）
rmse = mse ** (1/2)
print(rmse)

# 使用sklearn完成KNN模型
col = ['accommodates', 'bedrooms']
knn = KNeighborsRegressor()
# 将自变量和因变量传入模型进行训练，并使用测试集进行预测
knn.fit(norm_train_df[cols], norm_train_df['price'])
two_features_predictions = knn.predict(norm_test_df[cols])
# 计算预测值与实际值之间的均方根误差
two_features_mse = mean_squared_error(norm_test_df['price'], two_features_predictions)
two_features_rmse = two_features_mse ** (1/2)
print(two_features_rmse)

knn.fit()是KNeighborsRegressor模型（K近邻回归）的方法。它用于拟合（训练）模型，即将自变量和因变量传入模型进行训练。

在代码中，knn.fit(norm_train_df[cols], norm_train_df['price'])表示使用自变量norm_train_df[cols]（即特征列数据）和因变量norm_train_df['price']（即价格数据）来训练KNN模型。模型会根据训练数据学习相应的模式和关系，以便在之后进行预测。

如需要预测可以:

1
2
3
4
5
6
7
8
9
10
11
# 假设你已经创建并训练了一个名为knn的KNN模型

# 准备待预测的样本数据（以特征列 'accommodates' 和 'bathrooms' 为例）
new_data = [[2, 1], [4, 2], [3, 1.5]]  # 这里假设有3个待预测样本，每个样本有两个特征

# 使用已训练的KNN模型进行预测
predictions = knn.predict(new_data)

# 打印预测结果
for i, prediction in enumerate(predictions):
    print(f"样本{i+1}的预测结果：{prediction}")