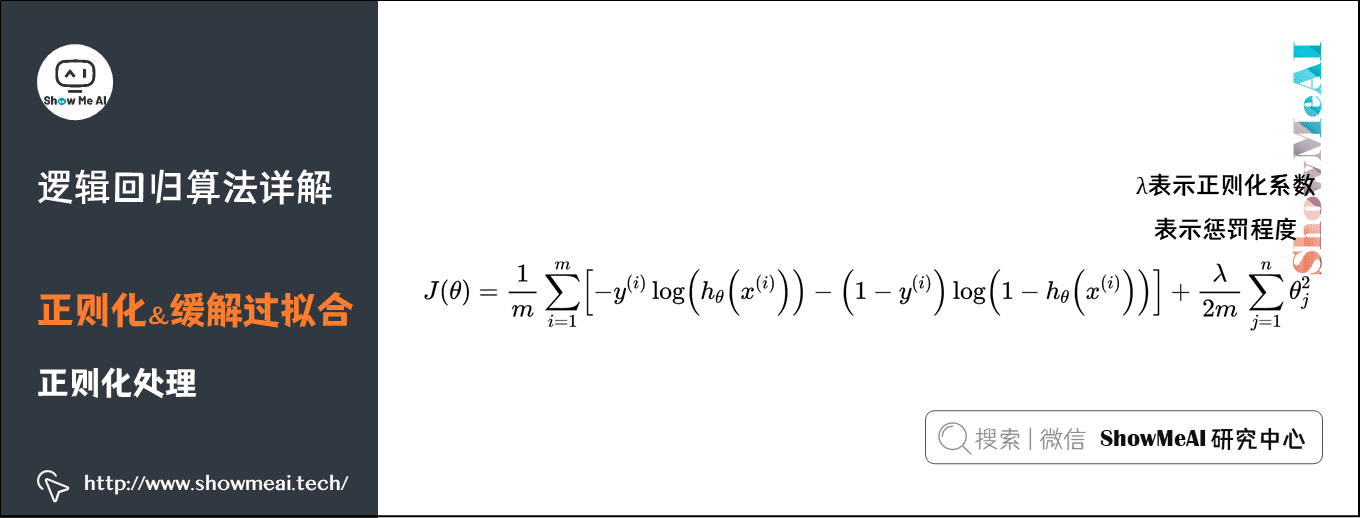ML-3-回归算法

算法核心思想

线性回归与分类

分类问题输出离散值(如是否垃圾），回归问题输出连续值（如房价）

• 分类方法：线性回归+阈值
  

逻辑回归核心思想

但是「线性回归+阈值」的方式很难得到鲁棒性好的分类器

逻辑回归将数据拟合到一个logit函数中，从而完成对事件发生概率的预测。

如果线性回归的结果输出是一个连续值，而值的范围是无法限定的，这种情况下我们无法得到稳定的判定阈值。那是否可以把这个结果映射到一个固定大小的区间内（比如 0~1 ），进而判断呢。

用于对连续值压缩变换的函数叫做 Sigmoid 函数（也称 Logistic 函数，S函数）。

Sigmoid 数学表达式为：$S(x)={\frac{1}{1+e^{-x}}}$
可以看到 $\ S$ 函数的输出值在 $\ 0$ 到 $\ 1$ 之间。

Sigmoid 函数与决策边界

决策边界就是分类器对于样本进行区分的边界，主要有线性决策和非线性决策

案例1：线性决策

如果我们用函数 $\ g$ 表示 Sigmoid 函数，逻辑回归的输出结果由假设函数$h_{\theta}(x)=g\left(\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}\right)$ 得到。

对于图中的例子，我们暂时取参数 $\theta_{0},\ \ \theta_{1},\ \ \theta_{2}$ 分别为$\ -3$ 、$\ 1$ 和 $\ 1$，那么对于图上的两类样本点，我们代入一些坐标到 $h_{\theta}(x)$ ，会得到什么结果值呢。

• 对于直线上方的点 $(x1,x2)$ 【例如（100，100）】，代入$-3+x_1+x_2$，得到大于 $\ 0$ 的取值，经过 Sigmoid 映射后得到的是大于 $\ 0.5$ 的取值
• 对于直线上方的点 $(x1,x2)$ 【例如（0，0）】，代入$-3+x_1+x_2$，得到大于 $\ 0$ 的取值，经过 Sigmoid 映射后得到的是小于 $\ 0.5$ 的取值
  以0.5为判定边界，那么 $-3+x_1+x_2$ 就是决策边界

案例2：非线性决策

我们用函数 $\ g$ 表示 Sigmoid 函数，逻辑回归的输出结果由假设函数 $h_{\theta}(x)=g\left(\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+\theta_{3}x_{1}^{2}+\theta_{4}x_{2}^{2}\right)$ 得到。

对于图中的例子，我们暂时取参数 $\theta_{0},\quad\theta_{1},\quad\theta_{2},\quad\theta_{3},\quad\theta_{4}$ 分别为 $\ -1$ 、 $\ 0$ 、 $\ 0$ 、 $\ 1$ 和 $\ 1$

可以发现在圆圈内的小于0.5，圆圈外大于0.5。
$-1+x_{1}^{2}+x_{2}^{2}=0$ 即是一条决策边界

梯度下降与优化

损失函数

线性

取不同的参数时，可以得到不同的决策边界。
哪一条决策边界是最好的？我们需要定义一个能量化衡量模型好坏的函数——损失函数（有时候也叫做「目标函数」或者「代价函数」）。我们的目标是使得损失函数最小化。

我们如何衡量预测值和标准答案之间的差异呢？ 均方误差

对于所有的样本点x，预测值 h(x) 与标准答案y作差后平方，求均值即可，这个取值越小代表差异度越小。

$$M S E={\frac{1}{m}}\sum_{i=1}^{m}\left(f\left(x_{i}\right)-y_{i}\right)^{2}$$

注意代价函数和MSE差了两倍。

逻辑回归

很遗憾， Sigmoid 函数的变换使得我们最终得到损失函数曲线非常不光滑凹凸不平，要找到最优参数（使得函数取值最小的参数）是很困难的

因此，在逻辑回归模型场景下，我们会改用对数损失函数（二元交叉熵损失）

$$J(\theta)=-\frac{1}{m}\left[\sum_{i=1}^{m}y^{(i)}\log h_{\theta}\left(x^{(i)}\right)+\left(1-y^{(i)}\right)\log\left(1-h_{\theta}\left(x^{(i)}\right)\right)\right]$$

其中 $y^{(i)}$ 表示样本取值，在其为正样本时取值为 $\ 1$，负样本时取值为0，我们分这两种情况来看看：

• $y^{(i)} = 0$：当一个样本为负样本时，若 $h_{\theta}(x)$ 的结果接近 $\ 1$ （即预测为正样本），那么$-\log!\left(1-h_{\theta}\left(x\right)\right)$ 的值很大，那么得到的惩罚就大
• 同理，为正样本但是预测结果接近0，惩罚也大

梯度下降

引入梯度

损失函数可以用于衡量模型参数好坏，但我们还需要一些优化方法找到最佳的参数

最常见的算法之一是「梯度下降法」，
逐步迭代减小损失函数（在凸函数场景下非常容易使用）。如同下山，找准方向（斜率），每次迈进一小步，直至山底。

对于一个非常简单的回归函数：y=wx+b
其中，x和y是已知的（训练集的已知量和标签），我们不断调整w(权重)和b(偏差)，然后再带入损失函数以求得最小值的过程，就是梯度下降。我们从-50开始到50结束设置w的值，我们通过随机数来是指偏置b

梯度可以完全理解为导数，梯度下降的过程就是我们不断求导的过程。

梯度下降算法原理

每次 θ1 更新都是减去一个 α与该点的斜率之积，当下降到局部最小处时，导数恰好为零，此时 θ1 不再更新，就得到了我们想要的结果

学习率（步长）

上图中，$\alpha$ 称为学习率（learning rate），直观的意义是，在函数向极小值方向前进时每步所走的步长。太大一般会错过极小值，太小会导致迭代次数过多。

学习率过大过小会怎么样？

步长是算法自己学习不出来的，它必须由外界指定。
这种算法不能学习，需要人为设定的参数，就叫做超参数。

特征缩放

加快梯度下降

多元线性回归，相比于单变量线性回归，该函数拥有多个变量值，那么他所拥有的参数就不仅仅是一个或者两个，而是多个。

$$h_{\theta}(x)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+\theta_{3}x_{3}+\dots+\theta_{n}x_{n}$$ $$h_{\theta}(x)=\left[\theta_{0}\qquad\theta_{1}\qquad\ldots\qquad\theta_{n}\right]\begin{bmatrix}x_1\\x_2\\ \ldots \\x_n\end{bmatrix}=\theta^{T}x$$

如果你想预测房价，现在有两个变量 x1 和 x2 来控制房子的价格。 x1 为房子的大小，范围在 0 到 2000，x2 为房子中卧室的数目，范围在 0 到 5，那么画出这个代价函数的轮廓图就是扁扁的椭圆形

红线比较曲折，需要缩短梯度下降时间

将变量 x1 和 x2 都缩放到一个范围中，我们将他们都缩放到 -1 到 1 这个范围内。随后使用归一化处理，使得其复合正态分布：

$$x_{n}={\frac{x_{n}-\mu_{n}}{s_{n}}}$$

过拟合和正则化

什么是过拟合

• 拟合曲线1：能正确分类，但仍有大量的样本未能正确分类，分类精度低，是「欠拟合」状态。
• 拟合曲线2：大部分样本正确分类，有足够的泛化能力，是较优的拟合曲线。
• 拟合曲线3：能够很好的将当前样本区分开来，但是当新来一个样本时，有很大的可能不能将其正确区分，原因是该决策边界太努力地学习当前的样本点，甚至把它们直接「记」下来了。

拟合曲线中的「抖动」，表示拟合曲线不规则、不光滑（上图中的拟合曲线3），对数据的学习程度深，过拟合了。

正则化

为了让代价函数最小，同时为了保留所有的特征，那么就可以给参数 θ 增加一个大的惩罚

这样要使代价函数最小，参数 θ_3 和 θ_4 就应该很小，因为它们的惩罚很大。当参数 θ_3 和 θ_4 很小时，在多项式中它们所在的那些项对整体影响就很小了

通过对损失函数添加正则化项，可以约束参数的搜索空间，从而保证拟合的决策边界并不会抖动非常厉害。(如下为逻辑回归的)

$\lambda$ 的值越大，为使$J(\theta)$ 的值小，则参数 $\ \theta$ 的绝对值就得越小，通常对应于越光滑的函数，也就是更加简单的函数，因此不易发生过拟合的问题。我们依然可以采用梯度下降对加正则化项的损失函数进行优化。

正则化的相关代价函数修正

• 线性回归

• 逻辑回归

代码实践

实践1：线性回归

from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt

# 创建线性回归模型对象
lr = LinearRegression()

# 拟合线性回归模型
X = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])  # 自变量 X
y = np.array([2, 4, 5, 8, 11, 13, 14, 16, 18, 20])  # 因变量 y
lr.fit(X.reshape(-1,1), y.reshape(-1,1))

# 准备测试数据
X_test = [[2.2], [2.6], [2.8]]
y_test = lr.predict(X_test)

# 准备预测数据
X_pred = 3 * np.random.rand(100, 1)
y_pred = lr.predict(X_pred)

# 绘制散点图和拟合曲线
plt.scatter(X, y, c='b', label='real')  # 绘制真实数据点
plt.plot(X_test, y_test, 'r', label='predicted point', marker='.', ms=20)  # 绘制测试数据点的预测结果
plt.plot(X_pred, y_pred, 'r-', label='predicted')  # 绘制随机预测数据点的预测结果
plt.xlabel("$X$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 3, 0, 15])
plt.legend(loc="upper left")

# 计算损失函数（均方误差）
loss = 0
for i in range(10):
    loss = loss + np.square(y[i] - lr.predict([[X[i]]]))  # 计算每个数据点的预测误差的平方并累加
plt.title("loss=%s" % loss)  # 显示损失函数的值

# 显示图形
plt.show()

实践2：听力损失

背景

该数据集，对5000名参与者进行了一项实验，以研究年龄和身体健康对听力损失的影响，尤其是听高音的能力。此数据显示了研究结果对参与者进行了身体能力的评估和评分，然后必须进行音频测试（通过/不通过），以评估他们听到高频的能力

• 特征：1. 年龄 2. 健康得分
• 标签：（1通过/0不通过）

import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

df = pd.read_csv('https://blog.caiyongji.com/assets/hearing_test.csv')
df.head()

sns.scatterplot(x='age',y='physical_score',data=df,hue='test_result')
sns.pairplot(df,hue='test_result')

age	physical_score	test_result
33	40.7	1
50	37.2	1
52	24.7	0
56	31	0
35	42.9	1

致做出判断，当年龄超过60很难通过测试，通过测试者普遍健康得分超过30

训练

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, classification_report, plot_confusion_matrix

# 准备数据
X = df.drop('test_result', axis=1)  # 特征矩阵 X,删除测试结果
y = df['test_result']  # 目标变量 y
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=50)  # 划分训练集和测试集

#标准化会将每个特征的值转换为均值为0，方差为1的标准正态分布，使得特征的值在相对较小的范围内
scaler = StandardScaler()  # 创建特征缩放器对象
scaled_X_train = scaler.fit_transform(X_train)  # 对训练集特征进行标准化缩放
scaled_X_test = scaler.transform(X_test)  # 对测试集特征进行标准化缩放

# 定义模型
log_model = LogisticRegression()  # 创建逻辑回归模型对象

# 训练模型
log_model.fit(scaled_X_train, y_train)  # 使用训练集数据拟合模型

# 预测数据
y_pred = log_model.predict(scaled_X_test)  # 对测试集进行预测
accuracy_score(y_test, y_pred)  # 计算分类准确率

我们经过准备数据，定义模型为LogisticRegression逻辑回归模型，通过fit方法拟合训练数据，最后通过predict方法进行预测。
最终我们调用accuracy_score方法得到模型的准确率为92.2%。

评估

plot_confusion_matrix(log_model,scaled_X_test,y_test)

• 真正类TP(True Positive) ：预测为正，实际结果为正。如，上图右下角285。
• 真负类TN(True Negative) ：预测为负，实际结果为负。如，上图左上角176。
• 假正类FP(False Positive) ：预测为正，实际结果为负。如，上图左下角19。
• 假负类FN(False Negative) ：预测为负，实际结果为正。如，上图右上角20。

实践3：鸢尾花分类（多标签|Softmax最大似然回归）

Logistic回归和Softmax回归都是基于线性回归的分类模型，两者无本质区别，都是从伯努利分结合最大对数似然估计

背景

该数据集，包含150个鸢尾花样本数据，数据特征包含花瓣的长度和宽度和萼片的长度和宽度，包含三个属种的鸢尾花，分别是山鸢尾(setosa)、变色鸢尾(versicolor)和维吉尼亚鸢尾(virginica)。

• 特征：1. 花萼长度 2. 花萼宽度 3. 花瓣长度 4 花萼宽度
• 标签：种类：山鸢尾(setosa)、变色鸢尾(versicolor)和维吉尼亚鸢尾(virginica)

df = pd.read_csv('https://blog.caiyongji.com/assets/iris.csv')
df.head()

sns.scatterplot(x='sepal_length',y='sepal_width',data=df,hue='species')
# 花萼 长度和宽度特征对应鸢尾花种类的散点图。

sns.scatterplot(x='petal_length',y='petal_width',data=df,hue='species')
# 花瓣 长度和宽度特征对应鸢尾花种类的散点图。

sns.pairplot(df,hue='species')
# 两两关系

sepal_length	sepal_width	petal_length	petal_width	species
5.1	3.5	1.4	0.2	setosa
4.9	3	1.4	0.2	setosa
4.7	3.2	1.3	0.2	setosa
4.6	3.1	1.5	0.2	setosa
5	3.6	1.4	0.2	setosa

综合考虑花瓣和花萼尺寸最小的为山鸢尾花，中等尺寸的为变色鸢尾花，尺寸最大的为维吉尼亚鸢尾花。

训练

# 准备数据
# 将'species'列从数据中移除，作为输入特征X
X = df.drop('species', axis=1)
# 将'species'列作为目标变量y
y = df['species']
# 使用train_test_split函数将数据集分为训练集和测试集，测试集占比为25%
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=50)
# 创建一个StandardScaler对象进行特征缩放
scaler = StandardScaler()
# 对训练集进行特征缩放处理，fit_transform()方法会计算训练集每个特征的均值和标准差，并进行缩放
scaled_X_train = scaler.fit_transform(X_train)
# 对测试集进行特征缩放处理，transform()方法使用训练集得到的均值和标准差进行缩放
scaled_X_test = scaler.transform(X_test)

# 定义模型
# 创建一个逻辑回归模型对象，使用'lbfgs'求解器进行多类别分类，参数C控制正则化强度，random_state用于重现结果
softmax_model = LogisticRegression(multi_class="multinomial", solver="lbfgs", C=10, random_state=50)

# 训练模型
# 使用训练集数据调用fit()方法来训练逻辑回归模型
softmax_model.fit(scaled_X_train, y_train)

# 预测数据
# 使用训练好的模型对缩放后的测试集进行预测
y_pred = softmax_model.predict(scaled_X_test)
# 使用accuracy_score函数计算预测准确率
accuracy_score(y_test, y_pred)

定义模型LogisticRegression的multi_class="multinomial"多元逻辑回归模型，设置求解器为lbfgs，通过fit方法拟合训练数据，最后通过predict方法进行预测。
最终我们调用accuracy_score方法得到模型的准确率为92.1%。

print(classification_report(y_test,y_pred))
# 查看准确率、精确度、召回率